如图，水平放置的正四棱柱形玻璃容器 $\mathrm{I}$ 和正四棱台形玻璃容器 $\mathrm{II}$ 的高均为 $32 \mathrm {cm}$，容器 $\mathrm{I}$ 的底面对角线 $AC$ 的长为 $10\sqrt 7 \mathrm {cm}$，容器 $\mathrm{II}$ 的两底面对角线 $EG$、$E_1G_1$ 的长分别为 $14 \mathrm {cm}$、$62 \mathrm {cm}$，分别在容器 $\mathrm{I}$ 和容器 $\mathrm{II}$ 中注入水，水深均为 $12 \mathrm {cm}$，现有一根玻璃棒 $l$，且长度为 $40 \mathrm {cm}$．（容器厚度，玻璃棒粗细均忽略不计．）
【难度】
【出处】
2017年高考江苏卷
【标注】
-
将 $l$ 放在容器 $\mathrm{I}$ 中，$l$ 的一端置于点 $A$ 处，另一端置于侧棱 $CC_1$ 上，求 $l$ 没入水中部分的长度；标注答案$16 \mathrm {cm}$解析由正棱柱的定义，知 $CC_1 \perp \text{ 平面}ABCD$，所以 $\text{平面}A_1ACC_1 \perp \text{ 平面}ABCD$，$CC_1 \perp AC$．
记玻璃棒的另一端落在 $CC_1$ 上点 $M$ 处．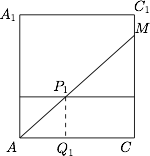
因为 $AC =10\sqrt 7$，$AM=40$，所以$$MC=\sqrt{40^2-(10\sqrt 7)^2}=30,$$从而 $\sin \angle MAC=\dfrac 34$．如图，记 $AM$ 与水面的交点为 $P_1$，过 $P_1$ 作 $P_1Q_1 \perp AC$，$Q_1$ 为垂足，则 $P_1Q_1\perp \text{平面}ABCD$，故 $P_1Q_1=12$，从而$$AP_1=\dfrac {P_1Q_1}{\sin \angle MAC}=16.$$ -
将 $l$ 放在容器 $\mathrm{II}$ 中，$l$ 的一端置于点 $E$ 处，另一端置于侧棱 $GG_1$ 上，求 $l$ 没入水中部分的长度．标注答案$20 \mathrm {cm}$解析如图，$O$，$O_1$ 是正棱台的两底面中心．
由正棱台的定义，知 $OO_1\perp \text{平面} EFGH$，所以 $\text{平面}E_1EGG_1\perp \text{平面}EFGH$，$O_1O\perp EG$．
同理，$\text{平面} E_1EGG_1\perp \text{平面}E_1F_1G_1H_1$，$O_1O\perp E_1G_1$．
记玻璃棒的另一端落在 $GG_1$ 上点 $N$ 处．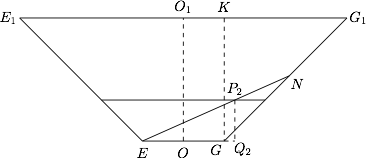
过 $G$ 作 $GK\perp E_1G$，$K$ 为垂足，则 $GK =OO_1=32$．
因为 $EG = 14$，$E_1G_1= 62$，
所以 $KG_1=\dfrac {62-14}{2}=24$，从而$$GG_1=\sqrt {KG)1^2+GK^2}=40.$$设 $\angle EGG_1=\alpha$，$\angle ENG =\beta$，则$$\sin \alpha=\sin \left(\dfrac {\pi}{2}+\angle KGG_1\right)=\dfrac 45.$$因为 $\dfrac {\pi}{2} < \alpha <\pi$，所以 $\cos \alpha=-\dfrac 35$．
在 $\triangle ENG$ 中，由正弦定理可得 $\dfrac {40}{\sin \alpha}=\dfrac {14}{\sin \beta}$，解得 $\sin \beta=\dfrac {7}{25}$．
因为 $0<\beta<\dfrac {\pi}{2}$，所以 $\cos \beta =\dfrac {24}{25}$．
于是$$\sin \angle NEG=\sin (\pi-\alpha-\beta)=\sin (\alpha+\beta)=\dfrac 35.$$记 $EN$ 与水面的交点为 $P_2$，过 $ P_2$ 作 $P_2Q_2\perp EG$，$Q_2$ 为垂足，则 $P_2Q_2\perp \text{平面} EFGH$，故 $P_2Q_2=12$，从而 $ EP_2=\dfrac {P_2Q_2}{\sin \angle NEG}=20$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
