如图,$AB$ 为半圆 $O$ 的直径,直线 $PC$ 切半圆 $O$ 于点 $C$,$AP\perp PC$,$P$ 为垂足.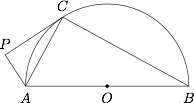

【难度】
【出处】
2017年高考江苏卷
【标注】
-
求证:$\angle PAC=\angle CAB$;标注答案略解析因为 $PC$ 切半圆 $O$ 于点 $C$,所以 $\angle PCA=\angle CBA$.
因为 $AB$ 为圆 $O$ 直径,所以 $\angle ACB=90^{\circ}$.
因为 $AP \perp PC$,所以 $\angle APC=90^{\circ}$.
所以 $\angle PAC=\angle CAB$. -
求证:$AC^2=AP \cdot AB$.标注答案略解析由第(1)小问知 $\triangle APC \backsim \triangle ACB$,故 $\dfrac {AP}{AC}=\dfrac {AC}{AB}$,所以 $AC^2=AP \cdot AB$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2