如图,已知四棱锥 $P-ABCD$,$\triangle PAD$ 是以 $AD$ 为斜边的等腰直角三角形,$BC \parallel AD$,$CD \perp AD$,$PC=AD=2DC=2CB$,$E$ 为 $PD$ 的中点.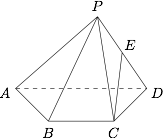

【难度】
【出处】
2017年高考浙江卷
【标注】
-
证明:$CE \parallel PAB$;标注答案略解析如图 ①,设 $PA$ 中点为 $F$,连结 $EF$,$FB$.
因为 $E$,$F$ 分别为 $PD$,$PA$ 中点,所以 $EF \parallel AD$ 且 $EF=\dfrac 12 AD$,
又因为 $BC \parallel AD$ 且 $BC=\dfrac 12 AD$,所以 $EF \parallel BC$ 且 $EF=BC$,
即四边形 $BCEF$ 为平行四边形,所以 $CE \parallel BF$,而 $CE \not \subset PAB$,$BF\subset PAB$,
因此 $CE \parallel PAB$.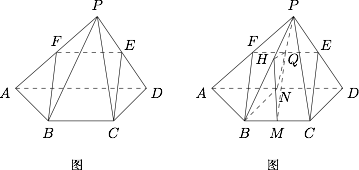
-
求直线 $CE$ 与平面 $PBC$ 所成角的正弦值.标注答案$\dfrac {\sqrt 2}{8}$解析如图 ②,分别取 $BC$、$AD$ 的中点 $M$、$N$.连结 $PN$ 交 $EF$ 于点 $Q$,过 $Q$ 作 $PB$ 的垂线,垂足为 $H$,连结 $MH$、$MQ$、$BN$.
因为 $E$、$F$、$N$ 分别是 $PD$、$PA$、$AD$ 的中点,所以 $Q$ 为 $EF$ 的中点.根据(1)易得 $MQ \parallel CE$.
因为 $\triangle PAD$ 是以 $AD$ 为斜边等腰直角三角形,$N$ 是 $AD$ 的中点,所以 $PN \perp AD$.
由 $CD \perp AD$,得 $BN \perp AD$,又 $BN \cap PN=N$,所以 $AD \perp \text{平面}PBN$,而 $BC\parallel AD$,所以 $BC \perp \text{平面}PBN$,因为 $QH \subset \text{平面}PBN$,所以 $BC \perp QH$,又因为 $QH \perp PB$,$PB \cap BC=B$,所以 $QH \perp \text{平面}PBC$,所以 $\angle QMH$ 为直线 $CE$ 与平面 $PBC$ 所成角.
设 $CD=1$,因为 $\triangle PAD$ 是以 $AD=2$ 为斜边的等腰直角三角形,所以 $PD=\sqrt 2$.在 $\triangle PCD$ 中,由余弦定理,得$$\cos \angle DPC=\dfrac {PD^2+PC^2-CD^2}{2PC \cdot PD}=\dfrac {5\sqrt 2}{8}.$$而在 $\triangle PCE$ 中,由余弦定理,得$$\cos \angle DPC=\dfrac {PE^2+PC^2-CE^2}{2PC \cdot PE} .$$解得 $CE=\sqrt 2$.同理可得 $PB=\sqrt 3$.
在 $\triangle PBN$ 中,由余弦定理,得$$\cos \angle BPN=\dfrac {PB^2+PN^2-BN^2}{2PB \cdot PN}=\dfrac {\sqrt 3}{2} .$$所以 $\angle BPN=30^{\circ}$,进而可得 $QH=\dfrac 14$,又 $MQ=\sqrt 2$,所以 $\sin\angle QMH=\dfrac {\sqrt 2}{8}$,即直线 $CE$ 与平面 $PBC$ 所成角的正弦值为 $\dfrac {\sqrt 2}{8}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2