如图,在三棱锥 $P-ABC$ 中,$PA\perp\mbox{底面}ABC$,$\angle BAC=90^\circ$.点 $D,E,N$ 分别为棱 $PA,PC,BC$ 的中点,$M$ 是线段 $AD$ 的中点,$PA=AC=4$,$AB=2$.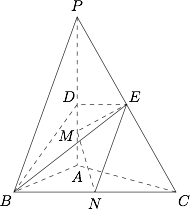

【难度】
【出处】
2017年高考天津卷(理)
【标注】
-
求证:$MN\parallel\mbox{平面}BDE$;标注答案略解析取 $AB$ 中点,记为 $I$,连接 $MI,NI$,如图.
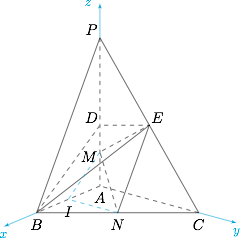 由 $M$ 为 $DA$ 中点,则 $MI$ 为 $\triangle ABD$ 的中位线,因此 $MI\parallel DB$;
由 $M$ 为 $DA$ 中点,则 $MI$ 为 $\triangle ABD$ 的中位线,因此 $MI\parallel DB$;
由 $N$ 为 $BC$ 中点,则 $NI$ 为 $\triangle ABC$ 的中位线,因此 $NI\parallel AC$,再结合 $D,E$ 为 $PA,PC$ 中点,则 $DE\parallel AC$,根据平行线的传递性,则 $NI\parallel DE$;
又 $MI\cap MI=I$,$DB\cap DE=D$,因此,面 $BDE\parallel \text{平面} MIN$,又 $MN\subset \text{平面}MIN$,因此 $MN\parallel \text{平面}BDE$. -
求二面角 $C-EM-N$ 的正弦值;标注答案$\dfrac{\sqrt{105}}{21}$解析因为 $PA\perp \text{平面}ABC$,$AC\perp AB$,因此 $AP,AB,AC$ 两两垂直,所以可以 $A$ 为原点,$AB,AC,AP$ 分别为 $x,y,z$ 轴,建立空间直角坐标系,如上图.
依题意可得$$E(0,2,2),M(0,0,1),N(1,2,0),\overrightarrow{EM}=(0,-2,-1),\overrightarrow{MN}=(1,2,-1),$$容易知道 $\overrightarrow{m}=(1,0,0)$ 为平面 $CEM$ 的一个法向量.
设 $\overrightarrow{n}=(x,y,z)$ 为平面 $EMN$ 的一个法向量,则$$\begin{cases}\overrightarrow{n}\cdot\overrightarrow{EM}=0,\\ \overrightarrow{n}\cdot\overrightarrow{MN}=0\end{cases}\text{即} \begin{cases}-2y-z=0,\\x+2y-z=0\end{cases}$$不妨设 $y=1$,解得 $\overrightarrow{n}=(-4,1,-2)$.
设二面角 $C-EM-N$ 的平面角为 $\theta$,则 $\theta\in[0,\pi]$,此时有$$|\cos\theta|=\left|\cos\left\langle\overrightarrow{m},\overrightarrow{n}\right\rangle\right|=\left|\dfrac{\overrightarrow{m}\cdot\overrightarrow{n}}{|\overrightarrow{m}|\cdot|\overrightarrow{n}|}\right|=\dfrac{4}{\sqrt{21}},$$根据同角三角函数基本关系式及 $\theta$ 的范围,得$$\sin\theta=\sqrt{1-\cos^2\theta}=\dfrac{\sqrt{105}}{21},$$所以二面角 $C-EM-N$ 的正弦值为 $\dfrac{\sqrt{105}}{21}$. -
已知点 $H$ 在棱 $PA$ 上,且直线 $NH$ 与直线 $BE$ 所成角的余弦值为 $\dfrac{\sqrt7}{21}$,求线段 $AH$ 的长.标注答案$\dfrac85$ 或 $\dfrac12$解析设 $AH=h$,则 $h\in[0,4]$,此时有 $H(0,0,h)$,因此$$\overrightarrow{NH}=(-1,-2,h),\overrightarrow{BE}=(-2,2,2),$$设直线 $NH$ 与直线 $BE$ 所成角为 $\alpha$,则 $\alpha\in\left[0,\dfrac{\pi}{2}\right]$,此时有$$\cos\alpha=|\cos\left\langle\overrightarrow{NH},\overrightarrow{BE}\right\rangle|=\left|\dfrac{\overrightarrow{NH}\cdot\overrightarrow{BE}}{|NH|\cdot|BE|}\right|=\dfrac{\sqrt7}{21},$$整理得$$10h^2-21h+8=0,$$解得 $h=\dfrac85$ 或 $h=\dfrac12$.
所以线段 $AH$ 的长为 $\dfrac85$ 或 $\dfrac12$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3