如图，直三棱柱 $ABC-A_1B_1C_1$ 的底面为直角三角形，两直角边 $AB$ 和 $AC$ 的长分别为 $4$ 和 $2$，侧棱 $AA_1$ 的长为 $5$．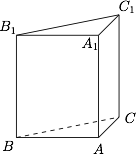
【难度】
【出处】
2017年高考上海卷
【标注】
-
（1）求三棱柱 $ABC-A_1B_1C_1$ 的体积；标注答案$20$解析根据棱柱体积公式，有$$V=sh=\dfrac12\cdot4\cdot2\cdot5=20.$$
-
（2）设 $M$ 是 $BC$ 的中点，求直线 $A_1M$ 与平面 $ABC$ 所成角的大小．标注答案$\arctan\sqrt5$解析如图，连接 $MA_1,MA$．
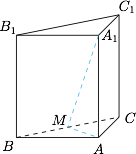由于直三棱柱，所以 $AA_1\perp\text{面}ABC$，故 $\angle A_1MA$ 即为直线 $A_1M$ 与平面 $ABC$ 所成角．
在 $\mathrm{Rt}\triangle ABC$ 中，$$BC=\sqrt{AB^2+AC^2}=2\sqrt5,$$结合 $M$ 为中点，则 $AM=\dfrac{BC}{2}=\sqrt5$，因此，在 $\mathrm{Rt}\triangle A_1MA$ 中，$$\tan\angle A_1MA=\dfrac{A_1A}{AM}=\dfrac{5}{\sqrt5}=\sqrt5,$$因此，直线 $A_1M$ 与平面 $ABC$ 所成角的大小为 $\arctan\sqrt5$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
