题目 如图，正方形 $ABCD$ 的中心为 $O$，四边形 $OBEF$ 为矩形，平面 $OBEF\perp 平面 ABCD$，点 $G$ 为 $AB$ 的中点，$AB=BE=2$． 问题1 求证：$EG\parallel 平面 ADF$； 答案1 略 解析1 考查线面平行的判定．由题意，$OF\perp 平面 ABCD$．如图，以 $O$ 为原点，分别以 $\overrightarrow {AD }$，$\overrightarrow {BA }$，$\overrightarrow {OF }$ 的方向为 $x$ 轴，$y$ 轴，$z$ 轴的正方向建立空间直角坐标系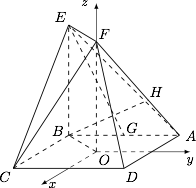．<img src="/static/images/2adbb1de3ca909a8da3a5bdda4270f03.png" class="img-responsive" />可得 $O\left(0,0,0\right)$，$A\left(-1,1,0\right)$，$B\left(-1,-1,0\right)$，$C\left(1,-1,0\right)$，$D\left(1,1,0\right)$，$E\left(-1,-1,2\right)$，$F\left(0,0,2\right)$，$G\left(-1,0,0\right)$．<br/>因为 $\overrightarrow {AD }=\left(2,0,0\right)$，$\overrightarrow {AF }=\left(1,-1,2\right)$，$\overrightarrow {EG }=\left(0,1,-2\right)$．<br/>设 $\overrightarrow {n_1}=\left(x_1,y_1,z_1\right)$ 为平面 $ADF$ 的法向量，则\[\begin{cases}\overrightarrow {n_1}\cdot \overrightarrow {AD}=0,\\ \overrightarrow {n_1}\cdot \overrightarrow {AF}=0,\end{cases}\]即\[\begin{cases}2x_1=0,\\ x_1-y_1+2z_1=0,\end{cases}\]不妨设 $z_1=1$，可得 $\overrightarrow {n_1}=\left(0,2,1\right)$．<br/>又因为 $\overrightarrow {EG }\cdot \overrightarrow {n_1 }=0$，且 $EG \not\subset 平面 ADF$，所以 $EG\parallel 平面 ADF$． 备注1 问题2 求二面角 $O-EF-C$ 的正弦值； 答案2 二面角 $O-EF-C$ 的正弦值为 $\dfrac {\sqrt 3}{3}$ 解析2 二面角的正弦值等于形成二面角的两个半平面的法向量夹角的正弦值．因为 $\overrightarrow {OA }=\left(-1,1,0\right)$，$\overrightarrow {EF }=\left(1,1,0\right)$，$\overrightarrow {CF }=\left(-1,1,2\right)$．易证 $\overrightarrow {OA }=\left(-1,1,0\right)$ 为平面 $OEF$ 的法向量．设 $\overrightarrow {n_2}=\left(x_2,y_2,z_2\right)$ 为平面 $ECF$ 的法向量，则\[\begin{cases}\overrightarrow {n_2}\cdot \overrightarrow {EF}=0,\\ \overrightarrow {n_2}\cdot \overrightarrow {CF}=0,\end{cases}\]即\[\begin{cases}x_2+y_2=0,\\ -x_2+y_2+2z_2=0,\end{cases}\]不妨设 $x_2=1$，可得 $\overrightarrow {n_2}=\left(1,-1,1\right)$．<br/>因此有\[\cos \langle \overrightarrow {OA },\overrightarrow {n_2 }\rangle =\dfrac {\overrightarrow {OA }\cdot \overrightarrow {n_2 }}{\left|\overrightarrow {OA }\right|\cdot |\overrightarrow {n_2 }|}=-\dfrac {\sqrt 6}{3}, \]于是 $\sin \langle \overrightarrow {OA },\overrightarrow {n_2 }\rangle =\dfrac {\sqrt 3}{3}$．<br/>所以二面角 $O-EF-C$ 的正弦值为 $\dfrac {\sqrt 3}{3}$ 备注2 问题3 设 $H$ 为线段 $AF$ 上的点，且 $AH=\dfrac{2}{3}HF$，求直线 $BH$ 和平面 $CEF $ 所成角的正弦值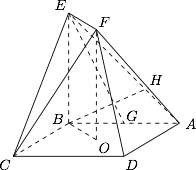．<img src="/static/images/aa49fb06e0a017c0e9455a59641f8ce2.png" class="img-responsive" /> 答案3 直线 $BH$ 和平面 $CEF $ 所成角的正弦值为 $\dfrac {\sqrt 7}{21}$ 解析3 所求值等于直线的方向向量与平面的法向量夹角余弦值的绝对值．由 $AH=\dfrac{2}{3}HF$，可得 $AH=\dfrac{2}{5}AF$．<br/>因为 $\overrightarrow {AF }=\left(1,-1,2\right)$，所以 $\overrightarrow {AH }=\left(\dfrac 25,-\dfrac 25,\dfrac 45\right)$，得 $H\left(-\dfrac 35,\dfrac 35,\dfrac 45\right)$，进而有 $\overrightarrow {BH }=\left(\dfrac 25, \dfrac 85,\dfrac 45\right)$．<br/>因此\[\cos \langle \overrightarrow {BH },\overrightarrow {n_2 }\rangle =\dfrac {\overrightarrow {BH }\cdot \overrightarrow {n_2 }}{\left|\overrightarrow {BH }\right|\cdot |\overrightarrow {n_2 }|}=-\dfrac {\sqrt 7}{21} .\]所以，直线 $BH$ 和平面 $CEF $ 所成角的正弦值为 $\dfrac {\sqrt 7}{21}$ 备注3