如图，在四棱锥 $P-ABCD$ 中，$AD\parallel BC$，$\angle ADC=\angle PAB=90^\circ$，$BC=CD=\dfrac12AD$．$E$ 为棱 $AD$ 的中点，异面直线 $PA$ 与 $CD$ 所成的角为 $90^\circ$．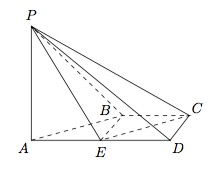
【难度】
【出处】
2016年高考四川卷（理）
【标注】
-
在平面 $PAB$ 内找一点 $M$，使得 直线 $ CM\parallel 平面 PBE$，并说明理由；标注答案略解析本题的关键在于通过思考得出“点 $M$ 在过 $C$ 且平行于平面 $PBE$ 的平面和平面 $PAB$ 的交线上”．延长 $AB$，交直线 $CD$ 于点 $M$，
因为 $E$ 为 $AD$ 中点，所以 $AE=ED=\dfrac{1}{2}AD$，
因为 $BC=CD=\dfrac{1}{2}AD$，所以 $ED=BC$，
因为 $AD\parallel BC$ 即 $ED\parallel BC$，所以四边形 $BCDE$ 为平行四边形，$BE\parallel CD$，
因为 $AB\cap CD=M$，所以 $M\in CD$，所以 $CM\parallel BE$，
因为 $BE\subset 面 PBE$，所以 $CM\parallel 面 PBE$，
因为 $M\in AB$，$AB\subset 面 PAB$，所以 $M\in 面 PAB$，
故在面 $PAB$ 上可找到一点 $M$ 使得 $CM\parallel 面 PBE$． -
若二面角 $P-CD-A$ 的大小为 $45^\circ$，求直线 $PA$ 与平面 $PCE$ 所成角的正弦值．标注答案$\dfrac13$解析本题考查线面角的求法，建立空间直角坐标系用向量的坐标表示求解是处理这类问题的核心做法．法一：
由已知，$CD\perp PA$，$CD\perp AD$，$PA\cap AD=A$，所以 $CD\perp 平面 PAD$．
于是 $CD\perp PD$，从而 $\angle PDA$ 是二面角 $P-CD-A$ 的平面角，所以 $\angle PDA=45^\circ$．
由 $PA\perp AB$，可得 $PA\perp 平面 ABCD$．
设 $BC=1$，则在 $\mathrm{Rt}\triangle PAD$ 中，$PA=AD=2$．
作 $Ay\perp AD$，以 $A$ 为原点，以 $\overrightarrow{AD},\overrightarrow{AP}$ 的方向分别为 $x$ 轴，$z$ 轴 的正方向，建立如图所示的空间直角坐标系 $A-xyz$．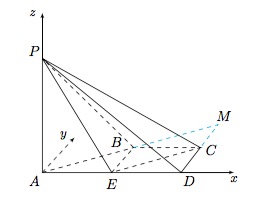
因此可得，$A\left(0,0,0\right),P\left(0,0,2\right),C\left(2,1,0\right),E\left(1,0,0\right)$，所以\[\overrightarrow{PE}=\left(1,0,-2\right),\overrightarrow{EC}=\left(1,1,0\right),\overrightarrow{AP}=\left(0,0,2\right),\]设平面 $PCE$ 的法向量为 $\overrightarrow{n}=\left(x,y,z\right)$，则\[\begin{cases}\overrightarrow{n}\cdot\overrightarrow{PE}=0,\\ \overrightarrow{n}\cdot\overrightarrow{EC}=0,\end{cases} 代入得 \begin{cases}x-2z=0,\\x+y=0,\end{cases}\]设 $x=2$，解得 $\overrightarrow{n}=\left(2,-2,1\right)$．
设直线 $PA$ 与平面 $PCE$ 所成角为 $\alpha$，则\[\sin\alpha=\dfrac{\left|\overrightarrow{n}\cdot\overrightarrow{AP}\right|}{|\overrightarrow{n}|\cdot\left|\overrightarrow{AP}\right|}=\dfrac13.\]所以直线 $PA$ 与平面 $PCE$ 所成角的正弦值为 $\dfrac13$．
法二：
过 $A$ 作 $AF\perp EC$ 交 $EC$ 于点 $F$，连接 $PF$，过 $A$ 作 $AG\perp PF$ 交 $PF$ 于点 $G$，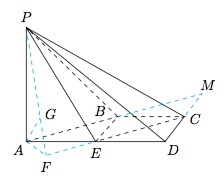
因为 $\angle PAB={{90}^{\circ }}$，$PA$ 与 $CD$ 所成角为 ${{90}^{\circ }}$，所以 $PA\perp AB$，$PA\perp CD$，
因为 $AB\cap CD=M$，所以 $PA\perp 面 ABCD$，
因为 $EC\subset 面 ABCD$，所以 $PA\perp EC$，
因为 $EC\perp AF$ 且 $AF\cap AP=A$，所以 $CE\perp 面 PAF$，
因为 $AG\subset 面 PAF$，所以 $AG\perp CE$，
因为 $AG\perp PF$ 且 $CE\cap PF=F$，所以 $AG\perp 面 PFC$，所以 $\angle APF$ 为所求 $PA$ 与面 $PCE$ 所成的角，
因为 $PA\perp 面 ABCD$，$\angle ADC={{90}^{\circ }}$ 即 $AD\perp DC$．所以 $\angle PDA$ 为二面角 $P-CD-A$ 所成的平面角，
由题意可得 $\angle PDA={{45}^{\circ }}$，而 $\angle PAD=90^{\circ }$，所以 $PA=AD$，
因为 $BC=CD$，四边形 $BCDE$ 是平行四边形，$\angle ADM={{90}^{\circ }}$，所以四边形 $BCDE$ 是正方形，
所以 $\angle BEC={{45}^{\circ }}$，所以 $\angle AEF=\angle BEC={{45}^{\circ }}$，
因为 $\angle AFE={{90}^{\circ }}$，所以 $AF=\dfrac{\sqrt{2}}{2}AE$，所以 $\tan \angle APF=\dfrac{AF}{AP}=\dfrac{\dfrac{\sqrt{2}}{4}AD}{AP}=\dfrac{\sqrt{2}}{4}$，$\sin \angle APF=\dfrac{1}{3}$．
因此，直线 $PA$ 与平面 $PCE$ 所成角的正弦值为 $\dfrac13$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
