如图，在四棱锥 $P-ABCD$ 中，平面 $PAD\perp $ 平面 $ABCD$，$PA\perp PD$，$PA=PD$，$AB\perp AD$，$AB=1$，$AD=2$，$AC=CD=\sqrt 5$．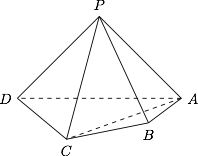
【难度】
【出处】
2016年高考北京卷（理）
【标注】
-
求证：$PD\perp$ 平面 $PAB$；标注答案略解析本题考查线面垂直，利用面面垂直的性质定理和已知条件即可证明．面 $PAD\cap \text{平面} ABCD=AD$，
面 $PAD\perp \text{平面}ABCD$，
因为 $AB\perp AD$，$AB\subset \text{平面}ABCD$，
所以 $AB\perp \text{平面}PAD$，
因为 $PD\subset \text{平面}PAD$，
所以 $AB\perp PD$，又 $PA\perp PD$，
所以 $PD\perp \text{平面}PAB$． -
求直线 $PB$ 与平面 $PCD$ 所成角的正弦值；标注答案$\dfrac{\sqrt{3}}{3}$解析本题可以利用空间向量来求解．取 $AD$ 的中点 $O$，连接 $CO$，$PO$．
因为 $CD=AC=\sqrt{5}$，所以 $CO\perp AD$，
因为 $PA=PD$，所以 $PO\perp AD$，
以 $O$ 为原点，建立如图坐标系：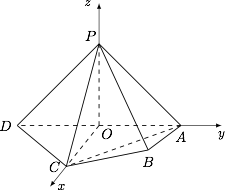
易知 $P\left( 0,0,1 \right)$，$B\left(1,1,0 \right)$，$D\left( 0,-1,0 \right)$，$C\left(2,0,0 \right)$，
则 $\overrightarrow{PB}=\left( 1,1,-1 \right)$，$\overrightarrow{PD}=\left(0,-1,-1 \right)$，$\overrightarrow{PC}=\left( 2,0,-1 \right)$，$\overrightarrow{CD}=\left(-2,-1,0 \right)$，
设平面 $PDC$ 的法向量为 $\overrightarrow{n}=\left({{x}_{1}},{{y}_{1}},1 \right)$，则\[\begin{cases}
\overrightarrow{n}\cdot \overrightarrow{PD}=0 \\
\overrightarrow{n}\cdot
\overrightarrow{PC}=0 \\
\end{cases}\]解得 $\overrightarrow{n}=\left( \dfrac{1}{2},-1,1\right)$，
设直线 $PB$ 与平面 $PCD$ 所成角为 $\theta $，则\[\begin{split}\sin
\theta &=\left| \cos \left\langle \overrightarrow{n},\overrightarrow{PB}
\right\rangle \right|=\left|
\frac{\overrightarrow{n}\cdot \overrightarrow{PB}}{\left| \overrightarrow{n}
\right|\cdot \left| \overrightarrow{PB} \right|} \right|\\&=\left| \frac{\frac{1}{2}-1-1}{\sqrt{\frac{1}{4}+1+1}\times
\sqrt{3}} \right|=\dfrac{\sqrt{3}}{3}.\end{split}\]所以直线 $PB$ 与平面 $PCD$ 所成角的正弦值为 $\dfrac{\sqrt{3}}{3}$． -
在棱 $PA$ 上是否存在点 $M$，使得 $BM\parallel \text{平面} PCD$？若存在，求 $\dfrac{AM}{AP}$ 的值；若不存在，说明理由．标注答案存在，$\dfrac{AM}{AP}=\dfrac{1}{4}$解析先假设存在，然后利用空间向量来证明．
假设存在 $M\left( 0,{{y}_{0}},{{z}_{0}} \right)$，使得 $BM\parallel \text{平面}PCD$，设 $\dfrac{AM}{AP}=\lambda $，$A\left(0,1,0 \right)$，$P\left( 0,0,1 \right)$，$B\left(1,1,0 \right)$．则 $\overrightarrow{AP}=\left(0,-1,1 \right)$，$\overrightarrow{AM}=\left(0,{{y}_{0}}-1,{{z}_{0}}\right)$，$\overrightarrow{AM}=\lambda \overrightarrow{AP}$，得 $M\left( 0,1-\lambda ,\lambda \right)$，$\overrightarrow{BM}=\left(-1,-\lambda ,\lambda \right)$，
因为 $BM\parallel \text{平面} PCD$，平面 $PDC$ 的法向量为 $\overrightarrow{n}$，
所以\[BM\cdot \overrightarrow{n}=0,\]即\[-\dfrac{1}{2}+\lambda +\lambda =0,\]解得\[\lambda
=\frac{1}{4},\]即当 $\dfrac{AM}{AP}=\dfrac{1}{4}$ 时，满足题意．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
