某公司计划购买 $2$ 台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个 $200$ 元.在机器使用期间,如果备件不足再购买,则每个 $500$ 元.现需决策在购买机器时应该同时购买几个易损零件,为此搜集并整理了 $100$ 台这种机器在三年使用期内更换的易损零件数,得下面柱状图: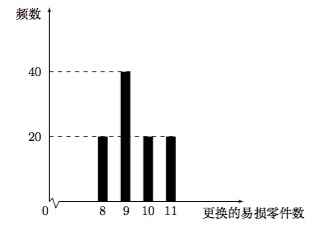 以这 $100$ 台机器更换的易损零件数的频率代替 $1$ 台机器更换的易损零件数发生的概率,记 $X$ 表示这 $2$ 台机器三年内共需要更换的易损零件数,$n$ 表示购买 $2$ 台机器的同时购买的易损零件数.
以这 $100$ 台机器更换的易损零件数的频率代替 $1$ 台机器更换的易损零件数发生的概率,记 $X$ 表示这 $2$ 台机器三年内共需要更换的易损零件数,$n$ 表示购买 $2$ 台机器的同时购买的易损零件数.
 以这 $100$ 台机器更换的易损零件数的频率代替 $1$ 台机器更换的易损零件数发生的概率,记 $X$ 表示这 $2$ 台机器三年内共需要更换的易损零件数,$n$ 表示购买 $2$ 台机器的同时购买的易损零件数.
以这 $100$ 台机器更换的易损零件数的频率代替 $1$ 台机器更换的易损零件数发生的概率,记 $X$ 表示这 $2$ 台机器三年内共需要更换的易损零件数,$n$ 表示购买 $2$ 台机器的同时购买的易损零件数.【难度】
【出处】
2016年高考全国乙卷(理)
【标注】
-
求 $X$ 的分布列;标注答案\[\begin{array}{|c|c|c|c|c|c|c|c|}\hline X&16&17&18&19&20&21&22\\ \hline P &0.04&0.16&0.24&0.24&0.2&0.08&0.04\\ \hline \end{array}\]解析本题考查离散型随机变量的分布列求法,根据频率分布直方图,得出对应概率即可.由柱状图可得:每台机器三年内可能更换的易损两件数为 $8$,$9$,$10$,$11$,概率分别为 $0.2$,$0.4$,$0.2$,$0.2$.
于是 $2$ 台机器三年内共需要更换的易损零件数 $X$ 可取 $16,17,18,19,20,21,22$.则\[\begin{split}&P\left(X=16\right)=0.2\times 0.2=0.04,\\& P\left(X=17\right)={\mathrm C}_{2}^{1}\times 0.2\times 0.4=0.16,\\& P\left(X=18\right)=0.2\times 0.2 +0.2\times 0.2+0.4\times 0.4=0.24,\\&P\left(X=19\right)=0.2\times 0.2 +0.4\times 0.2+0.4\times 0.2+0.2\times 0.2=0.24,\\&P\left(X=20\right)=0.2\times 0.2+0.4\times 0.2+0.2\times 0.4=0.2,\\& P\left(X=21\right)=0.2\times 0.2+0.2\times 0.2=0.08,\\& P\left(X=22\right)=0.2\times 0.2=0.04.\end{split}\]所以 $X$ 的分布列为\[\begin{array}{|c|c|c|c|c|c|c|c|}\hline X&16&17&18&19&20&21&22\\ \hline P &0.04&0.16&0.24&0.24&0.2&0.08&0.04\\ \hline \end{array}\] -
若要求 $P\left(X\leqslant n\right)\geqslant0.5$,确定 $n$ 的最小值;标注答案$19$解析根据 $(1)$ 小题的分布列,求出 $n$ 的最小值即可.$n$ 表示购买 $2$ 台机器的同时购买的易损零件数,则若使\[P\left(X\leqslant n\right)\geqslant 0.5,\]则 $n$ 的最小值为 $19$.因为 $P\left(X\leqslant 18\right)<0.5$,$P\left(X\leqslant 19\right)\geqslant 0.5$.
-
以购买易损零件所需费用的期望值为决策依据,在 $n=19$ 与 $n=20$ 之中选其一,应选用哪个?标注答案$19$解析分别计算出 $n=19$ 和 $n=20$ 时的费用的期望值比较即可.当 $n=19$ 时,费用的期望为 $19\times 200+500\times 0.2+1000\times 0.08+1500\times 0.04=4040$;
当 $n=20$ 时,费用的期望为 $20\times 200 +500\times 0.08+1000\times 0.04=4080$;
所以应选用 $n=19$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3