已知函数 $f\left(x\right)=|x+1|-|2x-3|$．
【难度】
【出处】
2016年高考全国乙卷（文）
【标注】
-
在答题卡第（24）题图中画出 $y=f\left(x\right)$ 的图象；
标注答案略解析本题考查绝对值函数的图象画法，具体做法为将绝对值去掉，得到分段函数，逐段画图象即可．函数 $f\left(x\right)=|x+1|-|2x-3|$，即 $f\left(x\right)=\begin{cases}x-4,&x\leqslant -1,\\ 3x-2,&-1 < x < \dfrac 32,\\ 4-x,&x\geqslant \dfrac 32.\end{cases}$ 图象如下：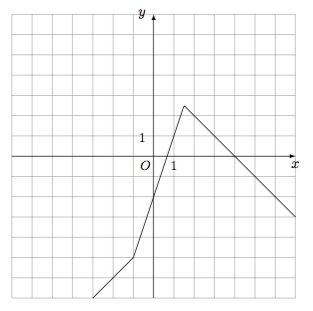
-
求不等式 $|f\left(x\right)|>1$ 的解集．标注答案$\left(-\infty,\dfrac 13\right)\cup \left(1,3\right)\cup \left(5,+\infty \right)$解析对于绝对值不等式逐段求解即可．对于不等式 $|f\left(x\right)|>1$．
当 $x\leqslant -1$ 时，$|x-4|>1$，解得 $x>5$ 或 $x<3$，所以此时 $x\leqslant -1$；
当 $-1 < x < \dfrac 32$ 时，$|3x-2|>1$，解得 $x>1$ 或 $x<\dfrac 13$，所以此时 $-1<x<\dfrac 13 $ 或 $ 1<x<\dfrac 32 $；
当 $x\geqslant \dfrac 32$ 时，$|4-x|>1$，解得 $x>5$ 或 $x<3$，所以此时 $\dfrac 32 \leqslant x <3$ 或 $x>5$．
综上，$x<\dfrac 13 $ 或 $ 1<x<3$ 或 $ x>5$．所以不等式 $|f\left(x\right)|>1$ 的解集为\[\left(-\infty,\dfrac 13\right)\cup \left(1,3\right)\cup \left(5,+\infty \right).\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
