如图，四棱锥 $P-ABCD$ 中，$PA\perp 底面 ABCD$，$AD\parallel BC$，$AB=AD=AC=3$，$PA=BC=4$，$M$ 为线段 $AD$ 上一点，$AM=2MD$，$N$ 为 $PC$ 的中点．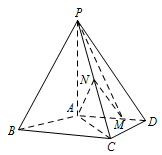
【难度】
【出处】
2016年高考全国丙卷（理）
【标注】
-
证明 $MN\parallel 平面 PAB$；标注答案略解析线面平行可利用线线平行来进行证明，本题就是构造平行四边形证明线线平行，进而得到线面平行．由已知得 $AM=\dfrac 23 AD=2$，
如图，取 $BP$ 中点 $T$，连接 $AT,TN$，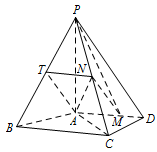
由 $N$ 为 $PC$ 的中点知 $TN\parallel BC$，且 $TN=\dfrac 12 BC=2$，
又 $AD\parallel BC$，故 $TN\parallel AM$，且 $TN=AM$，
所以四边形 $AMNT$ 为平行四边形，
所以 $MN\parallel AT$，
因为 $AT\subset 平面 PAB$，$MN \not\subset 平面 PAB$，
所以 $MN\parallel 平面 PAB$． -
求直线 $AN$ 与平面 $PMN$ 所成角的正弦值．标注答案$\dfrac{8\sqrt 5}{25}$解析建立空间直角坐标系，用向量法求解即可．取 $BC$ 中点 $E$，连接 $AE$，由 $AB=AC$ 得 $AE\perp BC$，从而 $AE\perp AD$，且\[AE=\sqrt{{AB}^2-{BE}^2}=\sqrt 5.\]以 $A$ 为坐标原点，$\overrightarrow {AE}$ 方向为 $x$ 轴正方向，建立如图所示的空间直角坐标系．
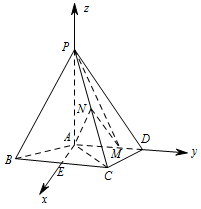由题意知，\[P\left(0,0,4\right),M\left(0,2,0\right),C\left(\sqrt 5,2,0\right),N\left(\dfrac{\sqrt 5}{2},1,2\right),\]\[\overrightarrow{PM}=\left(0,2,-4\right),\overrightarrow{PN}=\left(\dfrac {\sqrt 5}{2},1,-2\right),\overrightarrow{AN}=\left(\dfrac{\sqrt 5}{2},1,2\right).\]设 $\overrightarrow n=\left(x,y,z\right)$ 为平面 $PMN$ 的法向量，则\[\begin{cases}\overrightarrow n\cdot \overrightarrow{PM}=0,\\ \overrightarrow n\cdot \overrightarrow{PN}=0,\end{cases}\]即\[\begin{cases}2y-4z=0,\\\dfrac{\sqrt 5}{2}x+y-2z=0,\end{cases}\]取 $\overrightarrow n=\left(0,2,1\right)$，则\[\cos \left \langle\overrightarrow n,\overrightarrow {AN} \right \rangle=\dfrac {\overrightarrow n\cdot \overrightarrow {AN}}{\left|\overrightarrow n\right|\left|\overrightarrow {AN}\right|}=\dfrac{8\sqrt 5}{25}.\]所以直线 $AN$ 与平面 $PMN$ 所成角的正弦值为 $\dfrac{8\sqrt 5}{25}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
