如图,$A$,$B$,$C$ 三地有直道相通,$AB=5$ 千米,$AC=3$ 千米,$BC=4$ 千米.现甲、乙两警员同时从 $A$ 地出发匀速前往 $B$ 地,过 $t$ 小时,他们之间的距离为 $f\left(t\right)$(单位:千米).甲的路线是 $AB$,速度为 $5$ 千米/小时,乙的路线是 $ACB$,速度为 $8$ 千米/小时.乙到达 $B$ 地后在原地等待.设 $t=t_1$ 时,乙到达 $C$ 地.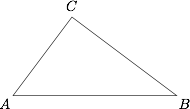

【难度】
【出处】
2015年高考上海卷(理)
【标注】
-
求 $t_1$ 与 $f\left(t_1\right)$ 的值;标注答案$t_1=\dfrac 38$;$f\left(t_1\right)=CD=\dfrac 38\sqrt{41}$(千米)解析$t_1=\dfrac 38$.
记乙到 $C$ 时甲所在地为 $D$,则 $AD=\dfrac{15}8$ 千米.
在 $\triangle ACD$ 中,$CD^2=AC^2+AD^2-2AC\cdot AD\cos A$,
所以 $f\left(t_1\right)=CD=\dfrac 38\sqrt{41}$(千米). -
已知警员的对讲机的有效通话距离是 $3$ 千米.当 $t_1\leqslant t\leqslant 1$ 时,求 $f\left(t\right)$ 的表达式,并判断 $f\left(t\right)$ 在 $\left[t_1,1\right]$ 上的最大值是否超过 $3$?说明理由.标注答案$f\left(t\right)$ 在 $\left[\dfrac 38,1\right]$ 上的最大值是 $\dfrac{3\sqrt{41}}{8}$,不超过 $3$.理由略解析甲到达 $B$ 用时 $1$ 小时;乙到达 $C$ 用时 $\dfrac 38$ 小时,从 $A$ 到 $B$ 总用时 $\dfrac 78$ 小时.
当 $t_1=\dfrac 38\leqslant t\leqslant \dfrac 78$ 时,\[ \begin{split}f\left(t\right)&=\sqrt{\left(7-8t\right)^2+\left(5-5t\right)^2-2\left(7-8t\right)\left(5-5t\right)\cdot \dfrac 45}\\&=\sqrt{25t^2-42t+18};\end{split} \]当 $\dfrac 78\leqslant t\leqslant 1$ 时,\[f\left(t\right)=5-5t.\]所以\[f\left(t\right)= \begin{cases}\sqrt{25t^2-42t+18},&\dfrac 38\leqslant t\leqslant \dfrac 78,\\
5-5t, & \dfrac 78<t\leqslant 1.
\end{cases} \]因为 $f\left(t\right)$ 在 $\left[\dfrac 38,\dfrac 78\right]$ 上的最大值是 $f\left(\dfrac 38\right)=\dfrac{3\sqrt{41}}{8}$,$f\left(t\right)$ 在 $\left[\dfrac 78,1\right]$ 上的最大值是 $f\left(\dfrac 78\right)=\dfrac{5}{8}$,
所以 $f\left(t\right)$ 在 $\left[\dfrac 38,1\right]$ 上的最大值是 $\dfrac{3\sqrt{41}}{8}$,不超过 $3$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2