如图所示，在多面体 $A_1B_1D_1DCBA$ 中，四边形 $AA_1B_1B$，$ADD_1A_1$，$ABCD$ 均为正方形，$E$ 为 $B_1D_1$ 的中点，过 $A_1$，$D$，$E$ 的平面交 $CD_1$ 于 $F$．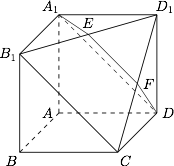
【难度】
【出处】
2015年高考安徽卷（理）
【标注】
-
证明：$EF\parallel B_1C_1$；标注答案略解析可通过线面平行来证明线线平行．由正方形的性质可知 $A_1B_1\parallel AB\parallel DC$，且 $A_1B_1=AB=DC$，所以四边形 $A_1B_1CD$ 为平行四边形，从而 $B_1C\parallel A_1D$．又 $A_1D\subset 平面A_1DE$，$B_1C\not\subset 平面A_1DE$，于是 $B_1C\parallel 平面A_1DE$．又 $B_1C\subset 平面B_1CD_1$，$平面 A_1DE\cap 平面B_1CD_1=EF$，所以 $EF\parallel B_1C$．
-
求二面角 $E-A_1D-B_1$ 的余弦值．标注答案二面角 $E-A_1D-B_1$ 的余弦值为 $\dfrac{\sqrt6}{3}$解析利用向量法结合图形求解二面角的余弦值．因为四边形 $AA_1B_1B$，$ADD_1A_1$，$ABCD$ 均为正方形，所以 $AA_1\perp AB$，$AA_1\perp AD$，$AB\perp AD$ 且 $AA_1=AB=AD$．
以 $A$ 为原点，分别以 $\overrightarrow{AB}$，$\overrightarrow{AD}$，$\overrightarrow{AA_1}$ 为 $x$ 轴，$y$ 轴和 $z$ 轴单位正向量建立如图所示的空间直角坐标系，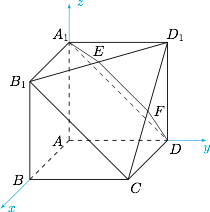
可得点的坐标 $A\left(0,0,0\right)$，$B\left(1,0,0\right)$，$D\left(0,1,0\right)$，$A_1\left(0,0,1\right)$，$B_1\left(1,0,1\right)$，$D_1\left(0,1,1\right)$，而 $E$ 点为 $B_1D_1$ 的中点，所以 $E$ 点的坐标为 $\left(0.5,0.5,1\right)$．
设面 $A_1DE$ 的法向量为 $\overrightarrow{n_1}=\left(r_1,s_1,t_1\right)$，而 $\overrightarrow{A_1E}=\left(0.5,0.5,0\right)$，$\overrightarrow{A_1D}=\left(0,1,-1\right)$，由 $\overrightarrow{n_1}\perp \overrightarrow{A_1E}$，$\overrightarrow{n_1}\perp\overrightarrow{A_1D}$，得 $r_1$，$s_1$，$t_1$ 应满足方程组\[\begin{cases}
0.5r_1+0.5s_1=0,\\s_1-t_1=0.
\end{cases}\]$\left(-1,1,1\right)$ 为其一组解，所以可取 $\overrightarrow{n_1}=\left(-1,1,1\right)$．
设面 $A_1B_1CD$ 的法向量为 $\overrightarrow{n_2}=\left(r_2,s_2,t_2\right)$，而 $\overrightarrow{A_1B_1}=\left(1,0,0\right)$，$\overrightarrow{A_1D}=\left(0,1,-1\right)$，由此同理可得 $\overrightarrow{n_2}=\left(0,1,1\right)$．结合图形知二面角 $E-A_1D-B_1$ 的余弦值为\[\dfrac{ \left|\overrightarrow{n_1}\cdot\overrightarrow{n_2} \right|}{ \left|\overrightarrow{n_1} \right|\cdot \left|\overrightarrow{n_2} \right|}=\dfrac{2}{\sqrt3\cdot \sqrt2}=\dfrac{\sqrt6}{3}.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
