如图,四边形 $ ABCD $ 为菱形,$ \angle ABC=120^\circ $,$ E $,$ F $ 是平面 $ ABCD $ 同一侧的两点,$ BE\perp 平面 ABCD $,$ DF\perp 平面 ABCD $,$ BE=2DF $,$ AE\perp EC $.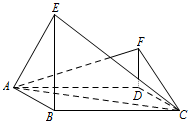

【难度】
【出处】
2015年高考全国Ⅰ卷(理)
【标注】
-
证明:$ 平面 AEC\perp 平面 AFC $;标注答案略解析此题易于建立空间坐标系,采用空间向量法解决;要证明两个面垂直只需证明两面法向量垂直即可.因为 $ ABCD$ 为菱形,所以 $ AC\perp BD$.
连接 $BD$,交 $ AC $ 于点 $O$.
以 $O$ 为原点,$\overrightarrow{OB}$ 为 $x$ 轴正方向,$\overrightarrow{OC}$ 为 $y$ 轴正方向,建立空间直角坐标系 $O-xyz$,则 $z$ 轴和 $BE$ 平行. 设菱形 $ABCD$ 边长为 $2$,$DF=h\left(h>0\right)$.
设菱形 $ABCD$ 边长为 $2$,$DF=h\left(h>0\right)$.
则 $A\left(0,-\sqrt3,0\right)$,$E\left(1,0,2h\right)$,$C\left(0,\sqrt3,0\right)$,$F\left(-1,0,h\right)$.
因为 $ AE\perp EC$,
所以 $\overrightarrow{AE}\cdot\overrightarrow{EC}=0$.
而 $\overrightarrow{AE}=\left(1,\sqrt3,2h\right)$,$\overrightarrow{EC}=\left(-1,\sqrt3,-2h\right)$,
所以 $-1+3-4h^2=0$,
解得 $ h=\dfrac{\sqrt2}{2}$,所以 $ F\left(-1,0,\dfrac{\sqrt2}{2}\right)$.
设面 $AEC$ 的法向量为 $\overrightarrow{m}=\left(x_1,y_1,z_1\right)$,面 $AFC$ 的法向量为 $\overrightarrow{n}=\left(x_2,y_2,z_2\right)$,
则\[\begin{cases}\overrightarrow{m}\cdot\overrightarrow{AC}=0,\\\overrightarrow{m}\cdot\overrightarrow{AE}=0,\end{cases}\]且\[\begin{cases}\overrightarrow{n}\cdot\overrightarrow{AC}= 0,\\\overrightarrow{n}\cdot\overrightarrow{AF}=0,\end{cases}\]而 $\overrightarrow{AC}=\left(0,2\sqrt3,0\right)$,$\overrightarrow{AE}=\left(1,\sqrt3,\sqrt2\right)$,$\overrightarrow{AF}=\left(-1,\sqrt3,\dfrac{\sqrt2}{2}\right)$.
所以\[\begin{cases}2\sqrt 3 y_1=0,\\x_1+\sqrt 3y_1+\sqrt 2z_1=0.\end{cases}\]且\[\begin{cases}2\sqrt 3y_2=0,\\-x_2+\sqrt 3y_2+\dfrac{\sqrt 2}{2}z_2=0.\end{cases}\]可求得 $\overrightarrow{m}=\left(\sqrt2,0,-1\right)$,$\overrightarrow{n}=\left(\sqrt2,0,2\right)$.
因为 $ \overrightarrow{m}\cdot\overrightarrow{n}=0$,
所以 $ 平面 AEC\perp 平面 AFC$. -
求直线 $ AE $ 与直线 $ CF $ 所成角的余弦值.标注答案$\dfrac{\sqrt3}{3}$解析空间直线的夹角可利用两条直线上的向量之间夹角求解.由 $(1)$ 知,$\overrightarrow{AE}=\left(1,\sqrt3,\sqrt2\right)$,$\overrightarrow{CF}=\left(-1,-\sqrt3,\dfrac{\sqrt2}{2}\right)$,所以\[\begin{split}{\left|{\cos\left\langle\overrightarrow{AE},\overrightarrow{CF}\right\rangle}\right|}&=\dfrac{{\left|{\overrightarrow{AE}\cdot\overrightarrow{CF}}\right|}}{{\left|{\overrightarrow{AE}}\right|}{\left|{\overrightarrow{CF}}\right|}}\\&=\dfrac{\sqrt3}{3}.\end{split}\]所以直线 $AE$ 和 $CF$ 所成角的余弦值为 $\dfrac{\sqrt3}{3}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2