如图，在四棱锥 $A-EFCB$ 中，$\triangle AEF$ 为等边三角形，$平面 AEF\perp \text{平面}EFCB$，$EF\parallel BC$，$BC=4$，$EF=2a$，$\angle EBC=\angle FCB=60^\circ$，$O$ 为 $EF$ 的中点．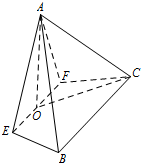
【难度】
【出处】
2015年高考北京卷（理）
【标注】
-
求证：$AO\perp BE$；标注答案略解析异面直线的垂直问题可以借助线面垂直来进行证明，本题中考虑 $AO\perp \text{平面}EFCB$ 可证．因为 $\triangle AEF$ 是等边三角形，$O$ 为 $EF$ 的中点，
所以 $AO\perp EF$．
又因为 $\text{平面} AEF\perp \text{平面}EFCB$，$AO\subset 平面AEF$，
所以 $AO\perp \text{平面}EFCB$，
所以 $AO\perp BE$． -
求二面角 $F-AE-B$ 的余弦值；标注答案$-\dfrac{\sqrt5}{5}$解析利用空间向量法求解两个面的法向量，然后计算二面角．取 $BC$ 的中点 $G$，连接 $OG$．
由题设知四边形 $FFCB$ 是等腰梯形，
所以 $OG\perp EF$．
由 $(1)$ 知 $AO\perp \text{平面}EFCB$．
又 $OG\subset \text{平面} EFCB$，
所以 $OA\perp OG$．
如图建立空间直角坐标系 $O-xyz$，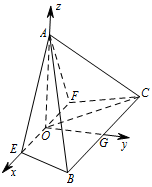
则 $E\left(a,0,0\right)$，$A\left(0,0,\sqrt3a\right)$，$B\left(2,\sqrt3\left(2-a\right),0\right)$，$\overrightarrow{EA}=\left(-a,0,\sqrt3a\right) $，$\overrightarrow {BE}=\left(a-2,\sqrt3\left(a-2\right),0\right)$．
设平面 $AEB$ 的一个法向量 $\overrightarrow n=\left(x,y,z\right)$，则\[\begin{cases}
\overrightarrow n\cdot\overrightarrow {EA}=0,\\\overrightarrow n\cdot\overrightarrow {BE}=0.
\end{cases}\]即\[\begin{cases}-ax+\sqrt3az=0,\\\left(a-2\right)x+\sqrt3\left(a-2\right)y=0.
\end{cases}\]令 $z=1$，则 $x=\sqrt3$，$y=-1$，于是 $\overrightarrow n=\left(\sqrt3,-1,1\right)$．
又平面 $AEF$ 的一个法向量为 $\overrightarrow p=\left(0,1,0\right)$，所以\[\begin{split}\cos \left\langle\overrightarrow n,\overrightarrow p\right\rangle& =\dfrac{\overrightarrow n\cdot\overrightarrow p}{ \left|\overrightarrow n \right| \left|\overrightarrow p \right|}\\&=-\dfrac{\sqrt5}{5} .\end{split}\]由题知二面角 $F-AE-B$ 为钝角，所以它的余弦值为 $-\dfrac{\sqrt5}{5}$． -
若 $BE\perp \text{平面}AOC$，求 $a$ 的值．标注答案$a=\dfrac43$解析利用线面垂直的性质建立向量数量积关系，求解未知量．因为 $BE\perp \text{平面}平面AOC$，
所以 $BE\perp CO$，即 $\overrightarrow {BE}\cdot\overrightarrow {OC}=0$．
因为 $\overrightarrow {BE}=\left(a-2,\sqrt3\left(a-2\right),0\right)$，$\overrightarrow {OC}=\left(-2,\sqrt3\left(2-a\right),0\right)$，
所以 $\overrightarrow {BE}\cdot\overrightarrow {OC}=-2\left(a-2\right)-3\left(a-2\right)^2$．
由 $\overrightarrow {BE}\cdot \overrightarrow {OC}=0$ 及 $0<a<2$，解得 $a=\dfrac43$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
