如图，已知四棱台 $ABCD-A_1B_1C_1D_1$ 的上、下底面分别是边长为 $3$ 和 $6$ 的正方形，$AA_1=6$，且 $AA_1\perp 底面 ABCD$，点 $P$，$Q$ 分别在棱 $DD_1$，$BC$ 上．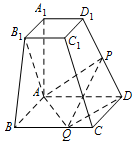
【难度】
【出处】
2015年高考湖南卷（理）
【标注】
-
若点 $P$ 是 $DD_1$ 的中点，证明：$AB_1\perp PQ$；标注答案略解析通过寻找线面垂直证明线线垂直．方法一：
由题设知 $AA_1$，$AD$，$AB$ 两两垂直，以 $A$ 为坐标原点，$AB$，$AD$，$AA_1$ 所在直线分别为 $x$ 轴，$y$ 轴，$z$ 轴，建立如图所示的空间直角坐标系．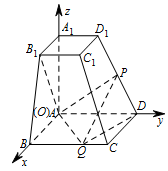
则相关各点的坐标为 $A\left(0,0,0\right)$，$B_1\left(3,0,6\right)$，$D\left(0,6,0\right)$，$D_1\left(0,3,6\right)$，$Q\left(6,m,0\right)$，其中 $m=BQ$，$0\leqslant m\leqslant 6$．
若点 $P$ 是 $DD_1$ 的中点，则 $P\left(0,\dfrac{9}{2},3\right)$，$\overrightarrow{PQ}=\left(6,m-\dfrac{9}{2},-3\right)$．
又 $\overrightarrow{AB_1}=\left(3,0,6\right)$，于是 $\overrightarrow{AB_1}\cdot\overrightarrow{PQ}=18-18=0$，
所以 $\overrightarrow{AB_1}\perp \overrightarrow{PQ}$，即 $AB_1\perp PQ$．
方法二：
如图，取 $AA_1$ 的中点 $R$，连接 $PR$，$BR$．
因为 $AA_1$，$DD_1$ 是梯形 $A_1 ADD_1$ 的两腰，$P$ 是 $D_1D$ 的中点，所以 $PR\parallel AD$，于是由 $AD\parallel BC$ 知，$PR\parallel BC$，所以 $P$，$R$，$B$，$C$ 四点共面．
由题设知 $BC\perp AB$，$BC\perp AA_1$，又 $AB\perp AA_1=\cap$，所以 $BC\perp 平面ABB_1A_1$，因此 $BC\perp AB_1 $．
因为 $\tan\angle ABR=\dfrac{AR}{AB}=\dfrac{3}{6}=\dfrac{A_1B_1}{A_1A}=\tan\angle A_1AB_1$，所以 $\angle ABR=\angle A_1AB_1$，因此 $\angle ABR+\angle BAB_1=\angle A_1AB_1+\angle BAB_1=90^\circ$，于是 $AB_1\perp BR$．又 $BC\cap BR=B$，知 $AB_1\perp 平面PRBC$．
又 $PQ\subset 平面 BRPC$，故 $AB_1\perp PQ$． -
若 $PQ\parallel 平面ABB_1A_1$，二面角 $P-QD-A$ 的余弦值为 $\dfrac{3}{7}$，求四面体 $ADPQ$ 的体积．标注答案$24$解析根据二面角为 $\dfrac37$，建立等式关系，求出 $Q$ 点坐标，再根据题中的线面平行条件，建立等式关系，求解出 $P$ 点坐标，利用三棱锥体积公式问题即可解决．由题设知，$\overrightarrow{DQ}=\left(6,m-6,0\right)$，$\overrightarrow{DD_1}=\left(0,-3,6\right)$ 是平面 $PQD$ 内两个不共线的向量．
设 $\overrightarrow{n_1}=\left(x,y,z\right)$ 是平面 $PQD$ 的一个法向量，则\[\begin{cases}
\overrightarrow{n_1}\cdot\overrightarrow{DQ}=0,\\
\overrightarrow{n_1}\cdot\overrightarrow{DD_1}=0,\\
\end{cases}\]代入得\[\begin{cases}6x+\left(m-6\right)y=0,\\
-3y+6z=0.\\
\end{cases}\]取 $y=6$，得 $\overrightarrow{n_1}=\left(6-m,6,3\right)$．
又平面 $AQD$ 的一个法向量是 $\overrightarrow{n_2}=\left(0,0,1\right)$，所以\[\begin{split}\cos\left \langle \overrightarrow{n_1},\overrightarrow{n_2}\right\rangle &\overset{\left[a\right]}=\dfrac{\overrightarrow{n_1}\cdot\overrightarrow{n_2}}{ \left|\overrightarrow{n_1} \right|\cdot \left|\overrightarrow{n_2} \right|}\\&=\dfrac{3}{\sqrt{\left(6-m\right)^2+6^2+3^2}\cdot 1}\\&=\dfrac{3}{\sqrt{\left(6-m\right)^2}+45}\end{split}\]（推导中用到[a]）
又二面角 $P-QD-A$的余弦值为 $\dfrac{3}{7}$，因此\[\dfrac{3}{\sqrt{\left(6-m\right)^2+45}}=\dfrac{3}{7},\]解得 $m=4$ 或 $m=8$（舍去），此时 $Q\left(6,4,0\right)$．
再设 $\overrightarrow{DP}=\lambda\overrightarrow{DD_1}\left(0<\lambda\leqslant 1\right)$，而 $\overrightarrow{DD_1}=\left(0,-3,6\right)$，由此得到 $P\left(0,6-3\lambda,6\lambda\right)$，所以 $\overrightarrow{PQ}=\left(6,3\lambda-2,-6\lambda\right)$．
因为 $PQ\parallel 平面ABB_1A_1$，且平面 $ABB_1A_1$ 的一个法向量是 $\overrightarrow{n_3}=\left(0,1,0\right)$，所以 $\overrightarrow{PQ}\cdot\overrightarrow{n_3}=0$，即 $3\lambda-2=0$，亦即 $\lambda=\dfrac{2}{3}$，从而 $P\left(0,4,4\right)$．
于是，将四面体 $ADPQ$ 视为 $\triangle ADQ$ 为底面的三棱锥 $P-ADQ$，其高 $h=4$，
故四面体 $ADPQ$ 的体积$V=\dfrac{1}{3}S_{\triangle ADQ}\cdot h=\dfrac{1}{3}\times\dfrac{1}{2}\times 6\times 6\times 4=24$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
