如图,在直三棱柱 $ABC-A_1B_1C_1$ 中,已知 $AC\perp BC$,$BC=CC_1$,设 $AB_1$ 的中点为 $D$,$B_1C\cap BC_1=E$.求证: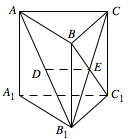

【难度】
【出处】
2015年高考江苏卷
【标注】
-
$DE\parallel 平面AA_1C_1C$;标注答案略解析本题可通过证明 $DE\parallel AC$ 来证明 $DE\parallel 面 AA_1C_1C$.由题意知,$E$ 为 $B_1C$ 的中点,
又 $D$ 为 $AB_1$ 的中点,因此 $DE\parallel AC$.
又因为 $DE\not\subset 平面AA_1C_1C$,$AC\subset 平面AA_1C_1C$,
所以 $DE\parallel 平面AA_1C_1C$. -
$BC_1\perp AB_1$.标注答案略解析可通过证明 $BC_1\perp 面 ACB_1$ 来证明 $BC_1\perp AB_1$.因为棱柱 $ABC-A_1B_1C_1$ 是直三棱柱,
所以 $CC_1 \perp 平面ABC$.
因为 $AC\subset 平面ABC$,
所以 $AC\perp CC_1$.
又因为 $AC\perp BC$,$CC_1\subset 平面BCC_1B_1$,$BC\subset 平面BCC_1B_1$,$BC\cap CC_1=C$,
所以 $AC\perp 平面BCC_1B_1$.
又因为 $BC_1\subset 平面BCC_1B_1$,
所以 $BC_1\perp AC$.
因为 $BC=CC_1$,
所以矩形 $BCC_1B_1$ 是正方形,因此 $BC_1\perp B_1C$.
因为 $AC,B_1C\subset 平面B_1AC$,$AC\cap B_1C=C$,
所以 $BC_1\perp 平面B_1AC$.
又因为 $AB_1\subset 平面B_1AC$,
所以 $BC_1\perp AB_1$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2