如图，在四棱锥 $P-ABCD$ 中，已知 $PA\perp 平面ABCD$，且四边形 $ABCD$ 为直角梯形，$\angle ABC=\angle BAD=\dfrac{\mathrm \pi} 2$，$PA=AD=2$，$AB=BC=1$．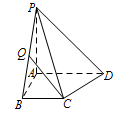
【难度】
【出处】
2015年高考江苏卷
【标注】
-
求平面 $PAB$ 与平面 $PCD$ 所成二面角的余弦值；标注答案$ \dfrac{\sqrt 3}{3} $解析本题可用向量法求解，注意 $\overrightarrow {AD}$ 是面 $PAB$ 的一个天然的法向量，只需要求面 $PCD$ 的法向量即可．建立如图所示的空间直角坐标系 $ A-xyz $，则各点的坐标为 $ B\left(1,0,0\right) $，$ C\left(1,1,0\right) $，$ D\left(0,2,0\right) $，$ P\left(0,0,2\right) $．
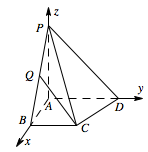由题意可证得 $ AD\perp 平面PAB $，所以 $ \overrightarrow{AD} $ 是平面 $ PAB $ 的一个法向量，$ \overrightarrow{AD}=\left(0,2,0\right) $．
计算得 $ \overrightarrow{PC}=\left(1,1,-2\right) $，$ \overrightarrow{PD}=\left(0,2,-2\right) $，
设平面 $ PCD $ 的法向量为 $ \overrightarrow{m}=\left(x,y,z\right) $，
则 $ \overrightarrow{m}\cdot \overrightarrow{PC}=0 $，$ \overrightarrow{m}\cdot \overrightarrow{PD}=0 $，
即 $ \begin{cases}
x+y-2z=0,\\2y-2z=0.
\end{cases} $ 令 $ y=1 $，解得 $ z=1 $，$ x=1 $．
所以 $ \overrightarrow{m}=\left(1,1,1\right) $ 是平面 $ PCD $ 的一个法向量．
从而 $ \cos \left\langle\overrightarrow{AD},\overrightarrow{m}\right\rangle=\dfrac{\overrightarrow{AD}\cdot \overrightarrow{m}}{{\left|{\overrightarrow{AD}}\right|}{\left|{\overrightarrow{m}}\right|}}=\dfrac{\sqrt 3}{3} $，
所以平面 $ PAB $ 与平面 $ PCD $ 所成二面角的余弦值为 $ \dfrac{\sqrt 3}{3} $． -
点 $Q$ 是线段 $BP$ 上的动点，当直线 $CQ$ 与 $DP$ 所成的角最小时，求线段 $BQ$ 的长．标注答案$\dfrac{2\sqrt 5}{5} $解析首先用参数将点 $Q$ 表达，然后表示出 $CQ$ 与 $DP$ 所成角的余弦值，研究它的最值，继而得到取最值时参数的值，从而求出 $BQ$ 长．算得 $ \overrightarrow{BP}=\left(-1,0,2\right) $．
因为 $Q$ 在 $BP$ 上，所以可设 $ \overrightarrow{BQ}=\lambda\overrightarrow{BP}=\left(-\lambda,0,2\lambda\right)\left(0\leqslant \lambda\leqslant 1\right) $，
又 $ \overrightarrow{CB}=\left(0,-1,0\right) $，则 $ \overrightarrow{CQ}=\overrightarrow{CB}+\overrightarrow{BQ}=\left(-\lambda,-1, 2\lambda\right) $．
又 $ \overrightarrow{DP}=\left(0,-2,2\right) $，
从而 $ \cos \left\langle\overrightarrow{CQ},\overrightarrow{DP}\right\rangle=\dfrac{\overrightarrow{CQ}\cdot \overrightarrow{DP}}{{\left|{\overrightarrow{CQ}}\right|}{\left|{\overrightarrow{DP}}\right|}}=\dfrac{1+2\lambda}{\sqrt{10\lambda^2+2}} $．
设 $ 1+2\lambda=t,t\leqslant \left[1,3\right] $，
则 $ \cos ^2\left\langle\overrightarrow{CQ},\overrightarrow{DP}\right\rangle=\dfrac{2t^2}{5t^2-10t+9}=\dfrac{2}{9\left(\dfrac 1t-\dfrac 59\right)^2+\dfrac{20}{9}}\leqslant \dfrac{9}{10} $．
当且仅当 $ t=\dfrac 95 $，即 $ \lambda=\dfrac 25 $ 时，等号成立．所以 $ {\left|{\cos \left\langle\overrightarrow{CQ},\overrightarrow{DP}\right\rangle}\right|}$ 的最大值为 $ \dfrac{3\sqrt{10}}{10} $．
因为 $ y=\cos x $ 在 $ \left(0,\dfrac{\mathrm \pi} {2}\right) $ 上是减函数，
所以此时直线 $ CQ $ 与 $ DP $ 所成角取得最小值．
又因为 $ BP=\sqrt{1^2+2^2}=\sqrt 5 $，
所以 $ BQ=\dfrac 25BP=\dfrac{2\sqrt 5}{5} $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
