已知函数 $f\left(x\right)$ 的图象是由函数 $g\left(x\right)=\cos x$ 的图象经如下变换得到：先将 $g\left(x\right)$ 图象上所有点的纵坐标伸长到原来的 $2$ 倍（横坐标不变），再将所得到的图象向右平移 $\dfrac{\mathrm \pi} 2$ 个单位长度．
【难度】
【出处】
2015年高考福建卷（理）
【标注】
-
求函数 $f\left(x\right)$ 的解析式，并求其图象的对称轴方程；标注答案$f\left(x\right)=2\sin x$；$x=k{\mathrm \pi} +\dfrac{\mathrm \pi} 2\left(k\in{\mathbb{Z}}\right)$解析本题考查三角函数的图象变换及三角函数的对称轴方程．将 $g\left(x\right)=\cos x$ 的图象上所有点的纵坐标伸长到原来的 $2$ 倍（横坐标不变）得到\[y=2\cos x,\]的图象，再将 $y=2\cos x$ 的图象向右平移 $\dfrac{\mathrm \pi} 2$ 个单位长度后得到\[y=2\cos\left(x-\dfrac{\mathrm \pi} 2\right),\]的图象，故 $f\left(x\right)=2\sin x$．
从而函数 $f\left(x\right)=2\sin x$ 的图象的对称轴方程为 $x=k{\mathrm \pi} +\dfrac{\mathrm \pi} 2\left(k\in\mathbb Z\right)$． -
已知关于 $x$ 的方程 $f\left(x\right)+g\left(x\right)=m$ 在 $\left[0,2{\mathrm \pi} \right)$ 内有两个不同的解 $\alpha$，$\beta$．
① 求实数 $m$ 的取值范围；
② 证明：$\cos\left(\alpha-\beta\right)=\dfrac{2m^2}5-1$．标注答案① $\left(-\sqrt 5,\sqrt 5\right)$；② 略解析通过辅助角公式将函数化为正弦型三角函数形式，再结合正弦函数的范围，得到 $m$ 范围；根据三角函数的对称性，将 $\alpha-\beta$ 统一成一个角，注意分类考虑，再结合二倍角公式即可解决．① 由 $(1)$ 知，\[\begin{split}f\left(x\right)+g\left(x\right)&=2\sin x+\cos x
\\&\overset{\left[a\right]}=\sqrt 5\sin\left(x+\varphi\right)\end{split}\]其中 $\sin\varphi =\dfrac{1}{\sqrt 5}$，$\cos\varphi =\dfrac{2}{\sqrt 5}$．
（推导中用到[a]）
根据正弦型函数的图象与性质，知 $\sin\left(x+\varphi\right)=\dfrac{m}{\sqrt 5}$ 在 $\left[0,2{\mathrm \pi} \right)$ 内有两个不同的解 $\alpha$，$\beta$，当且仅当 ${\left|{\dfrac m{\sqrt 5}}\right|}<1$，故 $m$ 的取值范围是 $\left(-\sqrt 5,\sqrt 5\right)$．
② 因为 $\alpha$，$\beta$ 是方程 $\sqrt 5\sin\left(x+\varphi\right)=m$ 在 $\left[0,2{\mathrm \pi} \right)$ 内的两个不同的解，所以\[\begin{split}&\sin\left(\alpha+\varphi\right)=\dfrac m{\sqrt 5},\\&\sin\left(\beta+\varphi\right)=\dfrac m{\sqrt 5},\end{split}\]画出 $h\left(x\right)=\sin\left(x+\varphi\right)$ 的图象如图所示．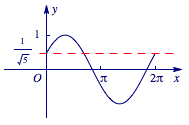
由上述图象可知，
当 $1\leqslant m<\sqrt 5$ 时，$\left(\alpha+\varphi\right)+\left(\beta+\varphi\right)=2\cdot \dfrac{\mathrm \pi} {2}$，即\[\alpha-\beta={\mathrm \pi} -2\left(\beta+\varphi\right);\]当 $-\sqrt 5< m<1$ 时，$\left(\alpha+\varphi\right)+\left(\beta+\varphi\right)=2\cdot \dfrac{3{\mathrm \pi} }{2}$，即\[\alpha-\beta=3{\mathrm \pi} -2\left(\beta+\varphi\right).\]因此，\[\begin{split}\cos\left(\alpha-\beta\right)&=-\cos {2\left(\beta+\varphi\right)}\\&\overset{\left[a\right]}=2{\sin^2}\left(\beta+\varphi\right)-1
\\&=\dfrac{2m^2}5-1.\end{split}\]（推导中用到[a]）
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
