《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑，如图，在阳马 $P-ABCD$ 中，侧棱 $PD\perp 底面ABCD$，且 $PD=CD$，过棱 $PC$ 的中点 $E$，作 $EF\perp PB$ 交 $PB$ 于点 $F$，连接 $DE$，$DF$，$BD$，$BE$．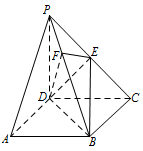
【难度】
【出处】
2015年高考湖北卷（理）
【标注】
-
证明：$PB\perp 平面DEF$．试判断四面体 $DBEF$ 是否为鳖臑，若是，写出其每个面的直角（只需写出结论）；若不是，说明理由．标注答案略解析理解鳖臑的定义，求证线线垂直即可．解法一：
因为 $PD\perp 底面ABCD$，
所以 $PD\perp BC$．
由底面 $ABCD$ 为长方形，有 $BC\perp CD$．
而 $PD\cap CD=D$，
所以 $BC\perp 平面PCD$．
而 $DE\subset 平面PCD$，
所以 $BC\perp DE$．
又因为 $PD=CD$，点 $E$ 是 $PC$ 的中点，
所以 $DE\perp PC$．
而 $PC\cap BC=C$，
所以 $DE\perp 平面PBC$．
而 $PB\subset 平面PBC$，
所以 $PB\perp DE$．
又 $PB\perp EF$，$DE\cap EF=E$，
所以 $PB\perp 平面DEF$．
由 $DE\perp 平面PBC$，$PB\perp 平面DEF$，可知四面体 $BDEF$ 的四个面都是直角三角形，即四面体 $BDEF$ 是一个鳖臑，其四个面的直角分别为 $\angle DEB$，$\angle DEF$，$\angle EFB$，$\angle DFB$．
解法二：
如图，以 $D$ 为原点，射线 $DA$，$DC$，$DP$ 分别为 $x$，$y$，$z$ 轴的正半轴，建立空间直角坐标系．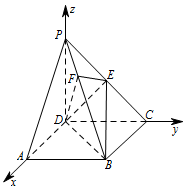
设 $PD=DC=1$，$BC=\lambda\left(\lambda>0\right)$，则 $D\left(0,0,0\right)$，$P\left(0,0,1\right)$，$B\left(\lambda,1,0\right)$，$C\left(0,1,0\right)$，$\overrightarrow{PB}=\left(\lambda,1,-1\right)$，
因为点 $E$ 是棱 $PC$ 的中点，
所以 $E\left(0,\dfrac 12,\dfrac 12\right)$，$\overrightarrow{DE}=\left(0,\dfrac 12,\dfrac 12\right)$，于是 $\overrightarrow{PB}\cdot \overrightarrow{DE}=0$，
所以 $PB\perp DE$．
又已知 $EF\perp PB$，而 $DE\cap EF=E$，
所以 $PB\perp 平面DEF$．
因为 $\overrightarrow{PC}=\left(0,1,-1\right)$，
所以 $\overrightarrow{DE}\cdot \overrightarrow{PC}=0$，
所以 $DE\perp PC$，而 $PB\cap PC=P$，
所以 $DE\perp 平面PBC$．
由 $DE\perp 平面PBC$，$PB\perp 平面DEF$，可知四面体 $BDEF$ 的四个面都是直角三角形，即四面体 $BDEF$ 是一个鳖臑，其四个面的直角分别为 $\angle DEB$，$\angle DEF$，$\angle EFB$，$\angle DFB$． -
若面 $DEF$ 与面 $ABCD$ 所成二面角的大小为 $\dfrac{\mathrm \pi} 3$，求 $\dfrac{DC}{BC}$ 的值．标注答案$\dfrac{\sqrt 2}2$解析求二面角的问题，关键在于构造出二面角的平面角．解法一：
如图，在面 $PBC$ 内，延长 $BC$ 与 $FE$ 交于点 $G$，则 $DG$ 是平面 $DEF$ 与平面 $ABCD$ 的交线．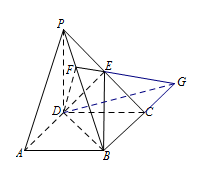
由 $(1)$ 知，$PB\perp 平面DEF$，
所以 $PB\perp DG$．
又因为 $PD\perp 底面ABCD$，
所以 $PD\perp DG$．
而 $PD\cap PB=P$，
所以 $DG\perp 平面PBD$．
故 $\angle BDF$ 是面 $DEF$ 与面 $ABCD$ 所成二面角的平面角．
设 $PD=DC=1$，$BC=\lambda\left(\lambda>0\right)$，有 $BD=\sqrt{1+\lambda^2}$，
在 $\mathrm {Rt}\triangle PDB$ 中，由 $DF\perp PB$，得 $\angle DPF=\angle FDB=\dfrac{\mathrm \pi} 3$，则\[\begin{split}\tan \dfrac{\mathrm \pi} 3&=\tan\angle DPF=\dfrac{BD}{PD}\\&=\sqrt{1+\lambda^2}\\&=\sqrt 3 ,\end{split}\]结合 $\lambda>0$ 解得 $\lambda=\sqrt 2$，所以\[\dfrac{DC}{BC}=\dfrac 1{\lambda}=\dfrac{\sqrt 2}2.\]故当面 $DEF$ 与面 $ABCD$ 所成二面角的大小为 $\dfrac{\mathrm \pi} 3$ 时，$\dfrac{DC}{BC}=\dfrac{\sqrt 2}2$．
解法二：
由 $PD\perp 平面ABCD$，所以 $\overrightarrow{DP}=\left(0,0,1\right)$ 是平面 $ABCD$ 的一个法向量．
由 $(1)$ 知，$PB\perp 平面DEF$，所以 $\overrightarrow{BP}=\left(-\lambda,-1,1\right)$ 是平面 $DEF$ 的一个法向量．
若面 $DEF$ 与面 $ABCD$ 所成二面角的大小为 $\dfrac{\mathrm \pi} 3$，则\[\cos\dfrac{\mathrm \pi} 3=\dfrac{\left|\overrightarrow{BP}\cdot \overrightarrow{DP}\right|}{\left|\overrightarrow{BP} \right|\left|\overrightarrow{DP}\right|}=\left|\dfrac{1}{\sqrt{\lambda^2+2}}\right|=\dfrac 12 ,\]结合 $\lambda>0$ 解得 $\lambda=\sqrt 2$，所以 $\dfrac{DC}{BC}=\dfrac 1{\lambda}=\dfrac{\sqrt 2}2$．
故当面 $DEF$ 与面 $ABCD$ 所成二面角的大小为 $\dfrac{\mathrm \pi} 3$ 时，$\dfrac{DC}{BC}=\dfrac{\sqrt 2}2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
