如图，在三棱柱 $ABC-A_1B_1C_1$ 中，$\angle BAC=90^\circ$，$AB=AC=2$，$A_1A=4$，$A_1$ 在底面 $ABC$ 的射影为 $BC$ 的中点，$D$ 是 $B_1C_1$ 的中点．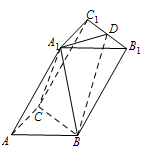
【难度】
【出处】
2015年高考浙江卷（理）
【标注】
-
证明：$A_1D\perp 平面A_1BC$；标注答案略解析按照线面垂直的判定，证明 $A_1D$ 和平面 $A_1BC$ 内的两条相交直线垂直即可．证明过程中，注意利用投影、中点、等腰三角形等条件．设 $ E $ 为 $ BC $ 的中点，连接 $ A_1E $，$AE $，$DE $．
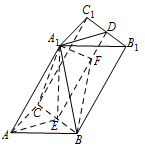由题意得 $ A_1E\perp 平面ABC $．
又因为 $ AE \subset 平面 ABC $，所以 $ A_1E\perp AE $．
因为 $ AB=AC $，所以 $ AE\perp BC $．
又因为 $A_1E \cap BC=E $，$A_1E\subset 平面 A_1BC $，$BC\subset 平面 A_1BC $．
所以 $ AE\perp 平面A_1BC $．
由 $ D$，$E $ 分别为 $ B_1C_1 $，$ BC $ 的中点，
得 $ DE\parallel B_1B $ 且 $ DE=B_1B $，从而 $ DE\parallel A_1A $，$ DE=A_1A $，
所以四边形 $ A_1AED $ 为平行四边形．
故 $ A_1D\parallel AE $．
又因为 $ AE\perp 平面A_1BC $，
所以 $ A_1D\perp 平面A_1BC $． -
求二面角 $A_1-BD-B_1$ 的平面角的余弦值．标注答案$-\dfrac 18$解析本题的难点在于构造出二面角的平面角，注意把空间的问题转化为平面的问题．法二中建系时注意选择三条两两垂直的直线．方法一：
作 $A_1F\perp BD$ 且 $A_1F\cap BD=F$，连接 $B_1F$．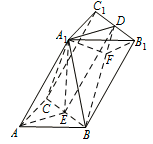
由 $AE=EB=\sqrt 2$，$\angle A_1EA=\angle A_1EB=90^\circ$，得 $A_1B=A_1A=4$．
由 $A_1D=B_1D$，$A_1B=B_1B$，得 $\triangle A_1DB$ 与 $\triangle B _1DB$ 全等．
由 $A_1F\perp BD$，得 $B_1F\perp BD$，因此 $\angle A_1FB_1$ 为二面角 $A_1-BD-B_1$ 的平面角．
由 $A_1D=\sqrt 2$，$A_1B=4$，$\angle DA_1B=90^\circ$，得 $BD=3\sqrt 2$，$A_1F=B_1F=\dfrac 43$．
由余弦定理得 $\cos\angle A_1FB_1=-\dfrac 18$．
方法二：
以 $CB$ 的中点 $E$ 为原点，分别以射线 $EA$，$EB$，$ EA_1 $ 为 $x$，$y$，$z $ 轴的正半轴，建立空间直角坐标系 $E-xyz$，如图所示．
由题意知各点坐标如下：
$A_1\left(0,0,\sqrt{14}\right)$，$B\left(0,\sqrt 2,0\right)$，$D\left(-\sqrt 2,0,\sqrt{14}\right)$，$B_1\left(-\sqrt 2,\sqrt 2,\sqrt{14}\right)$．
因此 $\overrightarrow{A_1B}=\left(0,\sqrt 2,-\sqrt{14}\right)$，$\overrightarrow{BD}=\left(-\sqrt 2,-\sqrt 2,\sqrt{14}\right)$，$\overrightarrow{DB_1}=\left(0,\sqrt 2,0\right)$．
设平面 $A_1BD$ 的法向量为 $\overrightarrow{m}=\left(x_1,y_1,z_1\right)$，平面 $B_1BD$ 的法向量为 $\overrightarrow{n}=\left(x_2,y_2,z_2\right)$．
由 $\begin{cases}
\overrightarrow{m}\cdot \overrightarrow{A_1B}=0,\\
\overrightarrow{m}\cdot \overrightarrow{BD}=0,
\end{cases}$ 即 $\begin{cases}\sqrt 2y_1-\sqrt{14}z_1=0,\\
-\sqrt 2x_1-\sqrt 2y_1+\sqrt{14}z_1=0.
\end{cases}$
可取 $\overrightarrow{m}=\left(0,\sqrt 7,1\right)$．
由 $\begin{cases}
\overrightarrow{n}\cdot \overrightarrow{DB_1}=0,\\
\overrightarrow{n}\cdot \overrightarrow{BD}=0,
\end{cases}$ 即 $\begin{cases}\sqrt 2y_2=0,\\
-\sqrt 2x_2-\sqrt 2y_2+\sqrt{14}z_2=0.
\end{cases}$
可取 $\overrightarrow{n}=\left(\sqrt 7,0,1\right)$．
于是 $\left|\cos \left\langle \overrightarrow{m},\overrightarrow{n}\right\rangle\right|=\dfrac{\left|\overrightarrow{m}\cdot \overrightarrow{n}\right|}{\left|\overrightarrow{m}\right|\cdot \left|\overrightarrow{n}\right|}=\dfrac 18$．
由题意可知，所求二面角的平面角是钝角，故二面角 $A_1-BD-B_1$ 的平面角的余弦值为 $-\dfrac 18$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
