如图，三角形 $PDC$ 所在的平面与长方形 $ABCD$ 所在的平面垂直，$PD=PC=4$，$AB=6$，$BC=3$．点 $E$ 是 $CD$ 边的中点，点 $F$，$G$ 分别在线段 $AB$，$BC$ 上，且 $AF=2FB$，$CG=2GB$．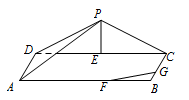
【难度】
【出处】
2015年高考广东卷（理）
【标注】
-
证明：$PE\perp FG$；标注答案略解析证明线线垂直一般通过线面垂直，已知 $PE\perp DC$，再结合要证明 $PE\perp FG$，故只需证明 $PE\perp $ 平面 $ABCD$ 即可．在 $\triangle PCD$ 中，因为 $ E$ 为 $CD$ 的中点，且 $PC=PD$，
所以 $PE\perp CD$．
又 $平面PCD\perp 平面ABCD$，且 $平面PCD\cap 平面ABCD=CD$，
所以 $PE\perp 平面ABCD$．
又 $FG\subset 平面ABCD$，所以 $ PE\perp FG$．
法二：
在 $\triangle PCD$ 中，因为 $E$ 为 $CD$ 的中点，且 $PC=PD$，
所以 $PE\perp CD$，又 $平面PCD\perp 平面ABCD$，且 $平面PCD\cap 平面ABCD=CD$，$PE\subset 平面PCD$，所以 $ PE\perp 平面ABCD$．
取 $AB$ 的中点 $H$，连接 $EH$．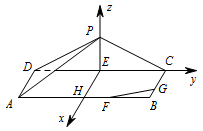
因为四边形 $ABCD$ 是长方体，所以 $EH\perp CD$．如图，以 $E$ 为原点，$EH$，$ EC $，$EP$ 所在直线分别为 $x$，$ y $，$z$ 轴建立空间直角坐标系，因为 $ PD=PC=4$，$AB=6$，$BC=3$，$AF=2FB$，$CG=2GB$，所以\[\begin{split} &E\left(0,0,0\right), P\left(0,0,\sqrt 7\right) ,F\left(3,1,0\right), \\ &G\left(2,3,0\right),A\left(3,-3,0\right), D\left(0,-3,0\right) ,\\& C\left(0,3,0\right).\end{split}\]因为 $\overrightarrow{EP}=\left(0,0,\sqrt 7\right)$，$\overrightarrow{FG}=\left(-1,2,0\right)$，所以\[\overrightarrow{EP}\cdot \overrightarrow{FG}=\left(0,0,\sqrt 7\right)\cdot\left(-1,2,0\right)=0,\]所以\[\overrightarrow{EP}\perp\overrightarrow{FG},\]即 $EP\perp FG$． -
求二面角 $P-AD-C$ 的正切值；标注答案二面角 $P-AD-C$ 的正切值为 $\dfrac{\sqrt 7}{3}$解析本小问是求二面角问题，可以用利用二面角的定义作出二面角，也可以通过向量法求得二面角．因为长方形 $ABCD$，所以 $AD\perp DC$．
又因为 $平面PCD\perp 平面ABCD$，且 $平面PCD\cap 平面ABCD=CD$，$AD\subset 平面ABCD$，
所以 $ AD\perp 平面PCD$．
所以 $ AD\perp PD$，$AD\perp DC$．
所以 $ \angle PDE$ 为二面角 $P-AD-C$ 的平面角．
因为 $AB=CD=6$，所以 $DE=3$．
在 $\mathrm {R}t\triangle PED$ 中，\[PE=\sqrt{PD^2-DE^2}=\sqrt{4^2-3^2}=\sqrt 7 ,\]所以\[\tan \angle PDE=\dfrac{PE}{DE}=\dfrac{\sqrt 7}{3},\]所以所求二面角 $P-AD-C$ 的正切值为 $\dfrac{\sqrt 7}{3}$．
法二：
因为 $ PE\perp 平面ABCD$，所以平面 $ABCD$ 的法向量为 $\overrightarrow{EP}=\left(0,0,\sqrt 7\right)$．
设平面 $ADP$ 的一个法向量为 $\overrightarrow n=\left(x_1,y_1,z_1\right)$，$\overrightarrow{AP}=\left(-3,3,\sqrt 7\right)$，$\overrightarrow{DP}=\left(0,3,\sqrt 7\right)$，由于\[\begin{cases}\overrightarrow{AP}\cdot\overrightarrow n=0,\\ \overrightarrow{DP}\cdot \overrightarrow n=0,\end{cases}\]即\[\begin{cases}-3x_1+3y_1+\sqrt 7z_1=0,\\ 3y_1+\sqrt 7z_1=0,\end{cases}\]令 $z_1=3$，则 $x_1=0$，$y_1=-\sqrt 7$，所以 $\overrightarrow n\left(0,-\sqrt 7,3\right)$．
由图可知二面角$P-AD-C$ 是锐角，设为 $\alpha$，则\[\cos\alpha\overset{\left[a\right]}={\left|{\dfrac{\overrightarrow n\cdot \overrightarrow{EP}}{{\left|{\overrightarrow{n}}\right|}{\left|{\overrightarrow{EP}}\right|}}}\right|}\overset{\left[a\right]}=\dfrac{3\sqrt 7}{4\sqrt 7}=\dfrac 34 ,\]（推导中用到：[a]）
所以 $\sin\alpha=\dfrac{\sqrt 7}{4}$，故 $\tan\alpha=\dfrac{\sqrt 7}{3}$． -
求直线 $PA$ 与直线 $FG$ 所成角的余弦值．标注答案直线 $PA$ 与 $FG$ 所成角的余弦值为 $\dfrac{9\sqrt 5}{25}$解析求异面直线的夹角，可以通过作平行线，构造三角形，通过余弦定理求得夹角，也可以通过向量的方法求其夹角．如图，连接 $AC$，
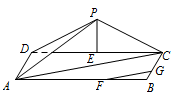在 $\triangle ABC$ 中，因为 $ AF=2FB$，$CG=2GB$，所以 $FG\parallel AC$．
由异面直线所成角的定义，知直线 $PA$ 与直线 $FG$ 所成角的大小等于 $\angle PAC$ 的大小．
在 $\mathrm {R}t\triangle PDA$ 中，\[\begin{split}&PA=\sqrt{PD^2+AD^2}=5, \\&AC=\sqrt{AB^2+BC^2}=3\sqrt 5 , \\&PC=4 .\end{split}\]所以\[\cos\angle PAC\overset{\left[b\right]}=\dfrac{PA^2+AC^2-PC^2}{2PA\cdot AC}=\dfrac{25+45-16}{2\times 5\times 3\sqrt 5}=\dfrac{9\sqrt 5}{25},\]（推导中用到：[b]）
所以直线 $PA$ 与直线 $FG$ 所成角的余弦值为 $\dfrac{9\sqrt 5}{25}$．
方法二：
因为 $ \overrightarrow{AP}=\left(-3,3,\sqrt 7\right)$，$\overrightarrow{FG}=\left(-1,2,0\right)$，设直线 $PA$ 与直线 $FG$ 所成角为 $\theta$．则\[\cos \theta\overset{\left[c\right]}={\left|{\dfrac{\overrightarrow{AP}\cdot \overrightarrow{FG}}{{\left|{\overrightarrow{AP}}\right|}{\left|{\overrightarrow{FG}}\right|}}}\right|}\overset{\left[c\right]}=\dfrac{3+6}{\sqrt{9+9+7}\times \sqrt 5}=\dfrac{9\sqrt 5}{25} .\]（推导中用到：[c]）
所以直线 $PA$ 与 $FG$ 所成角的余弦值为 $\dfrac{9\sqrt 5}{25}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
