如图，在三棱台 $DEF-ABC$ 中，$AB=2DE$，$G$，$H$ 分别为 $AC$，$BC$ 的中点．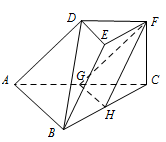
【难度】
【出处】
2015年高考山东卷（理）
【标注】
-
求证：$BD\parallel 平面FGH$；标注答案略解析此题属于线面平行的证明问题．证明线面平行可以通过构造平行四边形，中位线以及构造面面平行来证，过程中的法一是构造平行四边形来证明，法二是构造平行平面来证．证法一：
如图，连接 $DG$，$CD$，设 $CD\cap GF=O$，连接 $OH$．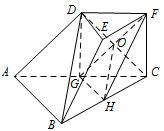
在三梭台 $DEF-ABC$ 中，$AB=2DE$，$G$ 为 $AC$ 的中点，可得 $DF \parallel GC$，$DF=GC$，
所以四边形 $DFCG$ 为平行四边形，则 $O$ 为 $CD$ 的中点．
又 $H$ 为 $BC$ 的中点，
所以 $OH \parallel BD$．
又 $OH\subset 平面FGH$，$BD\not\subset 平面FGH$，
所以 $BD \parallel 平面FGH$．
证法二：
在三棱台 $DEF-ABC$ 中，由 $BC=2EF$，$H$ 为 $BC$ 的中点，
可得 $BH \parallel EF$，$BH=EF$，
所以四边形 $BHFE$ 为平行四边形，可得 $BE \parallel HF$．
在 $\triangle ABC$ 中，$G$ 为 $AC$ 的中点，$H$ 为 $BC$ 的中点，
所以 $GH \parallel AB$．
又 $GH\cap HF=H$，
所以平面 $FGH \parallel 平面ABED$．
因为 $BD\subset 平面ABED$，
所以 $BD \parallel 平面FGH$． -
若 $CF\perp 平面ABC$，$AB\perp BC$，$CF=DE$，$\angle BAC=45^\circ$，求平面 $FGH$ 与平面 $ACFD$ 所成的角（锐角）的大小．标注答案$60^\circ$解析此题考查了求二面角，法一用向量法，法二几何法利用二面角定义作出二面角求解．解法一：
设 $AB=2$，则 $CF=1$．
在三棱台 $DEF-ABC$ 中，$G$ 为 $AC$ 的中点，
由 $DF=\dfrac 12AC=GC$，可得四边形 $DGCF$ 为平行四边形，因此 $DG \parallel FC$．
又 $FC \perp 平面ABC$，所以 $DG\perp 平面ABC$．
在 $\triangle ABC$ 中，因为 $AB\perp BC$，$\angle BAC=45^\circ$，$G$ 是 $AC$ 的中点，
所以 $AB=BC$，$GB\perp GC$，因此 $GB$，$GC$，$GD$ 两两垂直．
以 $G$ 为坐标原点建立如图所示的空间直角坐标系 $G-xyz$，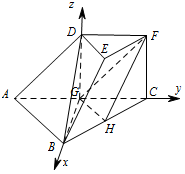
所以 $G\left(0,0,0\right)$，$B\left(\sqrt 2,0,0\right)$，$C\left(0,\sqrt 2,0\right)$，$D\left(0,0,1\right)$．
可得 $H\left(\dfrac {\sqrt 2}{2},\dfrac {\sqrt 2}{2},0\right)$，$F\left(0,\sqrt 2,1\right)$，故\[\begin{split}&\overrightarrow {GH}=\left(\dfrac {\sqrt 2}{2},\dfrac {\sqrt 2}{2},0\right) ,\\&\overrightarrow {GF}=\left(0,\sqrt 2,1\right).\end{split}\]设 $\overrightarrow n=\left(x,y,z\right)$ 是平面 $FGH$ 的一个法向量，则由\[\begin{cases}\overrightarrow n\cdot \overrightarrow {GH}=0,\\ \overrightarrow n\cdot \overrightarrow {GF}=0,
\end{cases}\]可得\[\begin{cases}\dfrac {\sqrt 2}{2}x+\dfrac {\sqrt 2}{2}y=0, \\ \sqrt 2 y+z=0.
\end{cases}\]令 $x=1$，可得平面 $FGH$ 的一个法向量 $\overrightarrow n=\left(1,-1,\sqrt 2\right)$．
因为 $\overrightarrow {GB}$ 是平面 $ACFD$ 的一个法向量，$\overrightarrow {GB}=\left(\sqrt 2,0,0\right)$，
所以\[\cos\left \langle \overrightarrow {GB},\overrightarrow n \right\rangle \overset{\left[a\right]}=\dfrac {\overrightarrow {GB}\cdot \overrightarrow n}{\left|\overrightarrow {GB}\right|\left|\overrightarrow n\right|}\overset{\left[a\right]}=\dfrac 12 .\]（推导中用到：[a]）
所以平面 $FGH$ 与平面 $ACFD$ 所成角（锐角）的大小为 $60^\circ$．
解法二：
如图，作 $HM\perp AC$ 于点 $M$，作 $MN\perp GF$ 于点 $N$，连接 $NH$．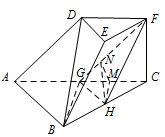
设 $AB=2$，则 $CF=1$．
由 $FC\perp 平面ABC$，得 $HM\perp FC$．
又 $FC\cap AC=C$，
所以 $HM\perp 平面ACFD$．
因此 $GF\perp NH$，
所以 $\angle MNH$ 为所求的二面角．
在 $\triangle BGC$ 中，$MH \parallel BG$，$MH=\dfrac 12BG=\dfrac {\sqrt 2}{2}$．
由 $\triangle GNM\backsim \triangle GCF$，可得 $\dfrac {MN}{FC}=\dfrac {GM}{GF}$，从而 $MN=\dfrac {\sqrt 6}{6}$．
由 $HM\perp 平面ACFD$，$MN\subset 平面ACFD$，得 $HM\perp MN$，
因此 $\tan \angle MNH=\dfrac {HM}{MN}=\sqrt 3$，
所以 $\angle MNH=60^\circ$．
所以平面 $FGH$ 与平面 $ACFD$ 所成角（锐角）的大小为 $60^\circ$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
