如图，三棱柱 $ABC - {A_1}{B_1}{C_1}$ 中，点 ${A_1}$ 在平面 $ ABC $ 内的射影 $ D $ 在 $ AC $ 上，$\angle ACB = {90^{\circ}}$，$BC = 1$，$AC = C{C_1} = 2$．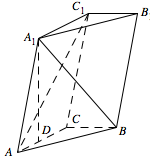
【难度】
【出处】
2014年高考大纲卷（文）
【标注】
-
证明：$A{C_1} \perp {A_1}B$；标注答案略．解析本小问考查的是线线垂直．空间中的线线垂直一般是通过线面垂直来证明的．${A_1}D \perp $ 平面 $ABC$，${A_1}D \subset $ 平面 $A{A_1}{C_1}C$，
故平面 $A{A_1}{C_1}C \perp $ 平面 $ABC$．
又 $BC \perp AC$，所以 $ BC \perp $ 平面 $A{A_1}{C_1}C$．
如图，连接 ${A_1}C$，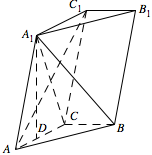
因为侧面 $A{A_1}{C_1}C$ 为菱形，故 $A{C_1} \perp {A_1}C$，
由 $BC \perp $ 平面 $A{A_1}{C_1}C$ 知 $AC_1 \perp BC$，
而 $A_1C \cap BC=C$，
故可得 $AC_1 \perp 面A_1CB$，所以 $A{C_1} \perp {A_1}B$． -
设直线 $A{A_1}$ 与平面 $BC{C_1}{B_1}$ 的距离为 $\sqrt 3 $，求二面角 ${A_1} - AB - C$ 的大小．标注答案$\arctan \sqrt {15} $．解析由二面角的概念，作出二面角的平面角，已知 $A_1D\perp $ 平面 $ABC$，故可以过 $D$ 作平面角，即可解得此题．$BC \perp $ 平面 $A{A_1}{C_1}C$，$BC \subset $ 平面 $BC{C_1}{B_1}$，
故平面 $A{A_1}{C_1}C \perp $ 平面 $BC{C_1}{B_1}$．
作 ${A_1}E \perp C{C_1}$，$E$ 为垂足，则 ${A_1}E \perp $ 平面 $BC{C_1}{B_1}$．
又直线 $A{A_1} \parallel $ 平面 $BC{C_1}{B_1}$，因而 ${A_1}E$ 为直线 $A{A_1}$ 与平面 $BC{C_1}{B_1}$ 的距离，${A_1}E = \sqrt 3 $．
因为 $A_1ACC_1$ 为菱形，故 ${A_1}D = {A_1}E = \sqrt 3 $．
作 $DF \perp AB$，$F$ 为垂足，连接 ${A_1}F$，
由题可知 $A_1D \perp 面 ACB$，所以 $A_1D \perp AB$．
因此，可知 $AB \perp 面 A_1DF$，因此 $A_1F \perp AB$，
故 $\angle {A_1}FD$ 为二面角 ${A_1} - AB - C$ 的平面角．
由\[AD = \sqrt {AA_1^2 - {A_1}{D^2}} = 1,\]得 $D$ 为 $AC$ 的中点，\[DF = \dfrac{1}{2} \times \dfrac{AC \times BC}{AB} = \dfrac{\sqrt 5 }{5},\]所以\[\tan \angle {A_1}FD = \dfrac{{{A_1}D}}{DF} = \sqrt {15} ,\]所以二面角 ${A_1} - AB - C$ 的大小为 $\arctan \sqrt {15} $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
