底面边长为 $ 2 $ 的正三棱锥 $P - ABC$,其表面展开图是三角形 ${P_1}{P_2}{P_3}$,如图,求 $\triangle {P_1}{P_2}{P_3}$ 的各边长及此三棱锥的体积 $V $.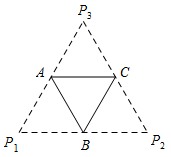

【难度】
【出处】
2014年高考上海卷(理)
【标注】
-
标注答案解析在 $\triangle {P_1}{P_2}{P_3}$ 中,\[{P_1}A = {P_3}A , {P_2}C = {P_3}C,\]所以 $AC$ 是 $\triangle {P_1}{P_2}{P_3}$ 的中位线,故\[{P_1}{P_2} = 2AC = 4.\]同理\[{P_2}{P_3} = {P_3}{P_1} = 4,\]所以 $\triangle {P_1}{P_2}{P_3}$ 是等边三角形,且边长为 $4$.
设 $Q$ 是 $\triangle ABC$ 的中心,则 $PQ \perp $ 平面 $ABC$,所以\[\begin{split}AQ & = \dfrac{2}{3}\sqrt 3 ,\\ PQ & = \sqrt {A{P^2} - A{Q^2}} = \dfrac{2}{3}\sqrt 6.\end{split}\]因此\[V = \dfrac{1}{3}{S_{\triangle ABC}} \cdot PQ = \dfrac{2}{3}\sqrt 2 .\]
题目
问题1
答案1
解析1
备注1