如图,四棱柱 $ABCD-{A_1}{B_1}{C_1}{D_1} $ 中,${A_1}A \perp 底面 ABCD$.四边形 $ABCD$ 为梯形,$AD \parallel BC$,且 $AD=2BC$.过 ${A_1}$,$C$,$D$ 三点的平面记为 $\alpha$,$B{B_1}$ 与 $\alpha$ 的交点为 $Q$.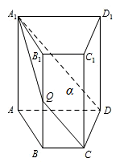

【难度】
【出处】
2014年高考安徽卷(理)
【标注】
-
证明:$Q$ 为 $B{B_1}$ 的中点;标注答案略.解析分析与中点有关的信息,由条件 $AD \parallel BC$,且 $AD=2BC$ 可联想到三角形的中位线,可延长 $DC$,$AB$ 交于点 $E$,连接 ${A_1}E$.易知 $A_1E \cap BB_1=Q$,且易证明出 $Q$ 为 $B{B_1}$ 的中点.延长 $DC$,$AB$ 交于点 $E$,连接 ${A_1}E$.
则 ${A_1}E$ 为平面 $\alpha $ 与平面 $AB{B_1}{A_1}$ 的交线.
而点 $Q$ 为 ${B_1}B$ 与平面 $\alpha $ 的交点,点 $Q$ 为平面 $\alpha $ 与平面 $AB{B_1}{A_1}$ 的公共点,所以点 $Q$ 在直线 ${A_1}E$ 上.
因为 $BC\parallel AD$,${C_1}C\parallel {D_1}D$,$BC \cap CC_1 = C$,$AD \cap {D_1}D = D$.
则有平面 ${B_1}{C_1}CB\parallel 平面 {A_1}{D_1}DA$.
平面 $\alpha $ 与平面 ${B_1}{C_1}CB$,平面 ${A_1}{D_1}DA$ 相交于 $CQ$,${A_1}D$,则 $CQ\parallel {A_1}D$.
又因为 $AD = 2BC$,所以 $CQ$ 为 $\triangle {A_1}DE$ 的中位线,所以 $Q$ 为 ${B_1}B$ 的中点.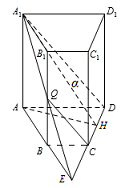
-
求此四棱柱被平面 $\alpha$ 所分成上下两部分的体积之比;标注答案四棱柱被平面 $\alpha$ 所分成上下两部分的体积之比 $\dfrac{V_上}{V_下}=\dfrac{11}{7}$.解析利用割补思想,把四棱柱被平面 $\alpha$ 所分为的下面那部分的几何体看成容易表示体积的三棱锥 $A_1-ADE$ 截掉三棱锥 $Q-BEC$.不妨设 $ABCD$ 的面积为 $S$,${A_1}A = h$.\[\begin{split}{V_下} &= {V_{{A_1} - ADE}} - {V_{Q - BCE}} \\& \overset {\left[a\right]}= \dfrac{1}{3} \cdot \dfrac{4}{3}Sh - \dfrac{1}{3} \cdot \dfrac{1}{3}S \cdot \dfrac{1}{2}h \\&= \dfrac{7}{18}Sh , \\ {V_上} &= V - {V_下} = Sh - \dfrac{7}{18}Sh \\&= \dfrac{11}{18}Sh,\end{split}\](推导中用到 $\left[a\right] $.)所以 $\dfrac{V_上}{V_下}=\dfrac{11}{7}$.
-
若 ${A_1}A=4$,$CD=2$,梯形 $ABCD$ 的面积为 $6$,求平面 $\alpha$ 与底面 $ABCD$ 所成二面角的大小.标注答案平面 $\alpha$ 与底面 $ABCD$ 所成二面角的大小为 ${45^ \circ }$.解析注意到 ${A_1}A \perp 底面 ABCD$,就可以根据三垂线定理容易的找到二面角的平面角.如图,过点 $ A $ 作 $AH \perp DE$ 于 $H$.
因为 $ AH \perp DE$,${A_1}A \perp DE$,${A_1}A \cap AH = A $,
所以 $ DE \perp 平面 {A_1}AH $,$ \therefore $ $ DE \perp {A_1}H $,
所以 $ \angle {A_1}HA $ 即为面 $ \alpha $ 和面 $ ABCD $ 所成二面角的平面角.
因为\[ {S_{\triangle {ADE}} }= \dfrac{4}{3}{S_{ABCD}} = \dfrac{1}{2}DE \cdot AH = 8,\]所以 $ AH = 4$,所以\[\tan \angle {A_1}HA=\dfrac{{{A_1}A}}{AH} = 1,\]所以 $\angle {A_1}HA = {45^ \circ }$,所以面 $ \alpha $ 和面 $ ABCD $ 所成二面角为 ${45^ \circ }$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3