如图，四棱锥 $P-ABCD$ 中，$ABCD$ 为矩形，平面 $PAD\perp 平面 ABCD$．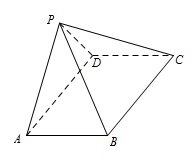
【难度】
【出处】
2014年高考江西卷（理）
【标注】
-
求证：$AB\perp PD$；标注答案略解析本题考查异面直线的垂直问题，借助线面垂直进行证明．因为 $ 面PAD \perp 面 ABCD $，$ AB \perp AD $，$ AD = 面 PAD \cap 面 ABCD $，所以 $ AB \perp 面 PAD $．又 $ PD\subset PAD $，故 $ AB \perp PD $．
-
若 $\angle BPC =90^\circ$，$PB = \sqrt 2 $，$PC=2$．问 $AB$ 为何值时，四棱锥 $P-ABCD$ 的体积最大？并求此时平面 $PBC$ 与平面 $DPC$ 夹角的余弦值．标注答案$ AB=\dfrac {\sqrt6} 3 $ 时，$ V_{P-ABCD}$ 最大；
平面 $PBC$ 与平面 $DPC$ 夹角的余弦值为 $ \dfrac {\sqrt {10}}{5} $解析本题考查二面角的计算，利用向量法进行求解．过 $ P $ 作 $ PO\perp AD $，所以 $ PO\perp 平面ABCD $．
作 $ OM\perp BC $ 于 $ M $，连接 $ PM $，所以 $ PM\perp BC $，
因为 $ \angle BPC=90^\circ $，$ PB=\sqrt 2$，$ PC=2 $，
所以 $ BC=\sqrt 6 $，$ PM=\dfrac{2}{\sqrt 3}=\dfrac{2\sqrt 3}{3}$，$ BM=\dfrac{\sqrt 6}{3}$．
设 $ AB=x $，所以 $ OM=x $，$ PO=\sqrt{\dfrac 4 3 -x^2}$，
所以\[\begin{split} V_{P-ABCD}&=\dfrac 1 3 \times x\times \sqrt 6 \times \sqrt{\dfrac 4 3 -x^2}\\&=\dfrac 1 3 \sqrt{8x^2-6x^4}.\end{split}\]当 $x^2=\dfrac 2 3 $，即 $ x=\dfrac {\sqrt6} 3 $ 时，$ {V_{P-ABCD}}$ 取得最大值．
建立如图所示的空间直角坐标系 $ O-xyz $：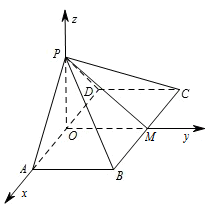
则 $ P\left(0,0,\dfrac {\sqrt6} 3 \right) $，$ D\left(-\dfrac{2\sqrt6}{3},0,0\right) $，$ C\left(-\dfrac{2\sqrt6}{3},\dfrac {\sqrt6} 3 ,0\right) $，
$ M\left(0,\dfrac {\sqrt6} 3 ,0\right) $，$B\left(\dfrac {\sqrt6} 3 ,\dfrac {\sqrt6} 3 ,0\right) $．
故 $ \overrightarrow {PC}=\left(-\dfrac{2\sqrt6}{3},\dfrac {\sqrt6} 3 ,-\dfrac {\sqrt6} 3\right) $，$ \overrightarrow {BC}=\left(- \sqrt6,0 ,0\right) $，$ \overrightarrow {DC}=\left(0,\dfrac {\sqrt6} 3 ,0\right) $．
设面 $ PBC $ 的法向量为 $\overrightarrow n=\left(x,y,z\right) $，则\[ \begin{cases}\overrightarrow n \perp \overrightarrow {PC},\\ \overrightarrow n \perp \overrightarrow {BC}.\end{cases} \]即\[ \begin{cases}-\dfrac{2\sqrt6}{3}x+\dfrac {\sqrt6} 3 y-\dfrac {\sqrt6} 3z=0,\\ -\sqrt 6x=0.\end{cases} \]令 $ y=1 $，得 $ x=0 $，$ z=1$，所以面 $ PBC $ 的法向量为 $\overrightarrow n=\left(0,1,1\right) $．
同理可得面 $ DPC $ 的法向量为 $\overrightarrow m=\left(1,0,-2\right) $．
所以\[\begin{split}\cos \left\langle \overrightarrow m,\overrightarrow n \right\rangle&=\dfrac{\overrightarrow n\cdot \overrightarrow m}{{\left|{\overrightarrow n}\right|}\cdot{\left|{\overrightarrow m}\right|}}\\&=\dfrac{-2}{\sqrt2\cdot\sqrt5}\\&=-\dfrac {\sqrt {10}}{5}.\end{split}\]又因为平面 $PBC$ 与平面 $DPC$ 的夹角为锐角，所以平面 $PBC$ 与平面 $DPC$ 夹角的余弦值为 $ \dfrac {\sqrt {10}}{5} $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
