如图,在四棱锥 $P - ABCD$ 中,$PA \perp 底面 ABCD$,$AD \perp AB$,$AB\parallel DC$,$AD = DC = AP = 2$,$AB = 1$,点 $E$ 为棱 $PC$ 的中点.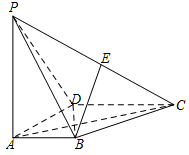

【难度】
【出处】
2014年高考天津卷(理)
【标注】
-
证明:$BE \perp DC$;标注答案略解析本题考查异面直线的垂直问题,可结合线面垂直加以证明.如图
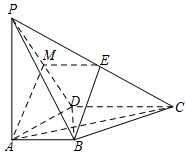 取 $PD$ 中点 $M$,连接 $EM$,$AM$.
取 $PD$ 中点 $M$,连接 $EM$,$AM$.
由于 $E$,$M$ 分别为 $PC$,$PD$ 的中点,故 $EM\parallel DC$ 且 $EM = \dfrac{1}{2}DC$.
又由已知,可得 $EM\parallel AB$ 且 $ EM = AB$,故四边形 $ABEM$ 为平行四边形,所以 $BE\parallel AM$.
因为 $PA \perp 底面 ABCD$,故 $PA \perp CD$,而 $CD \perp DA$,从而 $CD \perp 平面 PAD$.
因为 $AM \subset 平面 PAD$,于是 $CD \perp AM$.又 $BE\parallel AM$,所以 $BE \perp CD$. -
求直线 $BE$ 与平面 $PBD$ 所成角的正弦值;标注答案$\dfrac{\sqrt 3 }{3}$解析本题考查线面角的计算.需要用到第(1)结论 $CD\perp$ 平面 $PBD$,找到 $BE$ 与平面的线面角.如图,连接 $BM$.
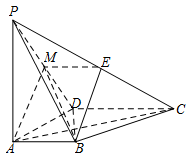 由(1)有 $CD \perp 平面 PAD$,而 $EM\parallel CD$,故 $ME \perp 平面 PAD$.所以 $PD \perp ME$.
由(1)有 $CD \perp 平面 PAD$,而 $EM\parallel CD$,故 $ME \perp 平面 PAD$.所以 $PD \perp ME$.
又因为 $AD = AP$,$M$ 为 $PD$ 的中点,故 $PD \perp AM$.又 $AM \cap ME=M$,所以 $PD \perp平面 BEM$,故平面 $BEM \perp 平面 PBD$.
所以直线 $BE$ 在平面 $PBD$ 内的射影为直线 $BM$,故 $\angle EBM$ 为直线 $BE$ 与平面 $PBD$ 所成的角.
而由(1)知 $BE \perp EM$,可得 $\angle EBM$ 为锐角,
依题意,有 $PD = 2\sqrt 2 $,而 $M$ 为 $PD$ 中点,
可得 $AM = \sqrt 2$,进而 $BE = \sqrt 2$,故在直角三角形 $BEM$ 中,\[\tan \angle EBM = \dfrac{EM}{BE} = \dfrac{1}{\sqrt 2 },\]所以,由同角三角函数的基本关系式得\[\sin \angle EBM = \dfrac{\sqrt 3 }{3},\]所以,直线 $BE$ 与平面 $PBD$ 所成角的正弦值为 $\dfrac{\sqrt 3 }{3}$. -
若 $F$ 为棱 $PC$ 上一点,满足 $BF \perp AC$,求二面角 $F - AB - P$ 的余弦值.标注答案$\dfrac{{3\sqrt {10} }}{10}$解析本题考查二面角的计算.根据条件可证 $AB\perp$ 平面 $PAD$,所以由二面角的定义可找到二面角的平面角.如图,在 $\triangle PAC$ 中,过点 $F$ 作 $FH\parallel PA$ 交 $AC$ 于点 $H$.
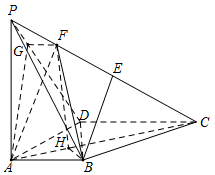 因为 $PA \perp $ 底面 $ABCD$,故 $FH \perp 底面 ABCD$,从而 $FH \perp AC$.
因为 $PA \perp $ 底面 $ABCD$,故 $FH \perp 底面 ABCD$,从而 $FH \perp AC$.
又 $BF \perp AC$,得 $AC \perp 平面 FHB$,因此 $AC \perp BH$.
在底面 $ABCD$ 内,可得 $CH = 3HA$,从而 $CF = 3FP$.
在平面 $PDC$ 内,作 $FG\parallel DC$ 交 $PD$ 于点 $G$,于是 $DG = 3GP$.
由于 $DC\parallel AB$,故 $GF\parallel AB$,所以 $A,B,F,G$ 四点共面.
由 $AB \perp PA$,$AB \perp AD$,得 $AB \perp $ 平面 $PAD$,故 $AB \perp AG$.
所以 $\angle PAG$ 为二面角 $F - AB - P$ 的平面角.
在 $\triangle PAG$ 中,可得\[PA = 2, PG = \dfrac{1}{4}PD = \dfrac{\sqrt 2 }{2}, \angle APG = {45^ \circ },\]由余弦定理可得\[AG = \dfrac{{\sqrt {10} }}{2},\cos \angle PAG = \dfrac{{3\sqrt {10} }}{10},\]所以,二面角 $F - AB - P$ 的余弦值为 $\dfrac{{3\sqrt {10} }}{10}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3