如图，四棱锥 $P - ABCD$ 中，底面 $ABCD$ 为矩形，$PA \perp 平面 ABCD$，$E$ 为 $PD$ 的中点．
【难度】
【出处】
2014年高考新课标Ⅱ卷（理）
【标注】
-
证明：$PB\parallel 平面 AEC$；标注答案略解析本题考查线面平行的证明．证明线面平行时，常常会构造中平行四边形，中位线或利用面面平行来证明，本题 $E$ 是 $PD$ 的中点，此图形是典型的利用中位线证明的题．如图，连接 $ BD $ 交 $ AC $ 于点 $ O $，连接 $ EO $．
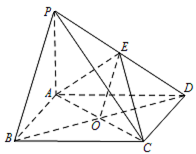因为 $ ABCD $ 为矩形，所以 $ O $ 为 $ BD $ 的中点．
又 $ E $ 为 $ PD $ 的中点，所以 $ EO\parallel PB $．
因为 $ EO \subset 平面 AEC $，$ PB \not\subset 平面 AEC $，所以 $ PB\parallel 平面 AEC $． -
设二面角 $D - AE - C$ 为 $60^\circ $，$AP = 1$，$AD = \sqrt 3 $，求三棱锥 $E - ACD$ 的体积．标注答案$ \dfrac{\sqrt 3 }{8}$解析利用二面角为 $60^\circ$，可利用空间向量的知识求得 $B$ 的坐标，进而求得三棱锥 $E-ACD$ 的高，然后利用三棱锥的体积公式，求得体积．因为 $ PA \perp 平面 ABCD $，$ ABCD $ 为矩形，所以 $ AB$，$AD$，$AP $ 两两垂直．
如图，以 $ A $ 为坐标原点，$\overrightarrow {AB} $ 的方向为 $ x $ 轴的正方向，$\left| {\overrightarrow {AP} } \right|$ 为单位长，建立空间直角坐标系 $A - xyz$，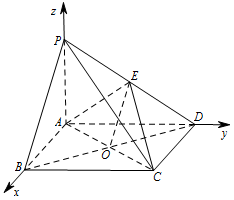
则\[D\left(0,\sqrt 3 ,0\right),E\left(0,\dfrac {\sqrt 3}{2} ,\dfrac12\right),\overrightarrow {AE}=\left(0,\dfrac {\sqrt 3}{2} ,\dfrac12 \right).\]设 $B\left(m,0,0\right)\left(m > 0\right)$，则\[C\left(m,\sqrt 3 ,0\right),\overrightarrow {AC} = \left(m,\sqrt 3 ,0\right).\]设 $\overrightarrow{n_1} = \left(x,y,z\right)$ 为平面 $ ACE $ 的法向量，则\[{\begin{cases}
\overrightarrow {n_1} \cdot \overrightarrow {AC} = 0, \\
\overrightarrow {n_1} \cdot \overrightarrow {AE} = 0, \\
\end{cases}}\]即\[{\begin{cases}mx + \sqrt 3 y = 0, \\
\dfrac{\sqrt 3 }{2}y + \dfrac{1}{2}z = 0, \\
\end{cases}}\]可取\[\overrightarrow{n_1} = \left(\dfrac{\sqrt 3 }{m}, - 1,\sqrt 3 \right).\]又 $\overrightarrow{n_2} = \left(1,0,0\right)$ 为平面 $ DAE $ 的法向量，由题设\[\left| {\cos \left\langle {\overrightarrow{n_1},\overrightarrow{n_2}} \right\rangle } \right| \overset{\left[a\right]}= \dfrac{1}{2},\]即\[\sqrt {\dfrac{3}{{3 + 4{m^2}}}} \overset{\left[b\right]}= \dfrac{1}{2},\]（推导中用到[a]，[b]）．
解得 $m = \dfrac{3}{2} $．
因为 $ E $ 为 $ PD $ 的中点，所以三棱锥 $E - ACD$ 的高为 $\dfrac{1}{2}$．
故三棱锥 $E - ACD$ 的体积\[V\overset{\left[a\right]}= \dfrac{1}{3} \times \dfrac{1}{2} \times \sqrt 3 \times \dfrac{3}{2} \times \dfrac{1}{2} = \dfrac{\sqrt 3 }{8}.\]（推导中用到[a]）
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
