如图，$P$ 是 $ \odot O$ 外一点，$PA$ 是切线，$A$ 为切点，割线 $PBC$ 与 $ \odot O$ 相交于点 $B$，$C$，$PC = 2PA$，$D$ 为 $PC$ 的中点，$AD$ 的延长线交 $ \odot O$ 于点 $E$．证明：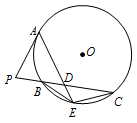
【难度】
【出处】
2014年高考新课标Ⅱ卷（理）
【标注】
-
$BE = EC$；标注答案略解析利用条件，考虑通过证明弦所对弧相等来进行证明．如图，连接 $ AB$，$AC $．
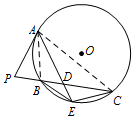由题设知 $ PA=PD $，故 $ \angle PAD=\angle PDA $．
因为\[ \begin{split}\angle PDA&=\angle DAC+\angle DCA,\\ \angle PAD&=\angle BAD+\angle PAB,\\\angle DCA&=\angle PAB,\end{split} \]所以 $ \angle DAC=\angle BAD $，从而 $\stackrel\frown{EB}= \stackrel\frown{EC}$．因此\[ BE=EC.\] -
$AD \cdot DE = 2P{B^2}$．标注答案略解析本题考查圆幂定理的应用．由切割线定理得\[P{A^2} = PB \cdot PC.\]因为 $ PA=PD=DC $，所以\[ \begin{split}DC&=2PB,\\BD&=PB.\end{split} \]由相交弦定理得\[AD \cdot DE = BD \cdot DC,\]所以\[AD \cdot DE = 2P{B^2}.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
