四面体 $ABCD$ 及其三视图如图所示，过棱 $AB$ 的中点 $E$ 作平行于 $AD$，$BC$ 的平面分别交四面体的棱 $BD$，$ DC$，$ CA$ 于点 $F $，$ G $，$ H$．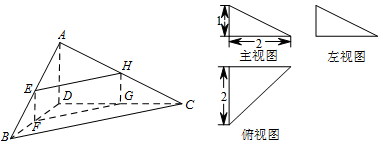
【难度】
【出处】
2014年高考陕西卷（理）
【标注】
-
证明：四边形 $EFGH$ 是矩形；标注答案略．解析可将 $BC$ 和 $AD$ 作为寻找四边形 $EFGH$ 四条边的位置关系的桥梁．由该四面体的三视图可知，$BD \perp DC$，$BD \perp AD$，$AD \perp DC$，$BD = DC = 2$，$AD = 1$．
由题设，$BC\parallel 面 EFGH$，
面 $EFGH \cap 面 BDC = FG$，
面 $EFGH \cap 面 ABC = EH$，
所以 $ BC\parallel FG$，$BC\parallel EH$，所以 $FG\parallel EH$．
同理 $EF\parallel AD$，$HG\parallel AD$，所以 $ EF \parallel HG$．
所以四边形 $EFGH$ 是平行四边形．
又因为 $ BD \perp AD$，$AD \perp DC$，$BD \cap DC = D$，
所以 $AD \perp 平面 BDC$，
所以 $ AD \perp BC$，
因为 $ BC\parallel FG$，$EF\parallel AD$，
所以 $ EF \perp FG$，
所以四边形 $EFGH$ 是矩形． -
求直线 $AB$ 与平面 $EFGH$ 夹角 $\theta $ 的正弦值．标注答案$ \dfrac{{\sqrt {10} }}{5}$．解析可用向量法求线面角，求出 $\overrightarrow {AB}$ 的方向向量和面 $EFGH$ 的法向量，然后利用向量夹角公式求解．如图，
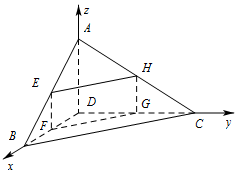以 $D$ 为坐标原点建立空间直角坐标系 $D-xyz$，则\[D\left(0,0,0\right) , A\left(0,0,1\right) , B\left(2,0,0\right) , C\left(0,2,0\right) , \]则根据向量的坐标运算得\[\overrightarrow {DA} = \left(0,0,1\right), \overrightarrow {BC} = \left( - 2,2,0\right), \overrightarrow {BA} = \left( - 2,0,1\right).\]设平面 $EFGH$ 的一个法向量$\overrightarrow n = \left(x,y,z\right)$，
因为 $ BC\parallel FG$，$EF\parallel AD$，所以\[\overrightarrow n \cdot \overrightarrow {DA} = 0, \overrightarrow n \cdot \overrightarrow {BC} = 0,\]即\[\begin{cases}
{z = 0} ,\\
{ - 2x + 2y = 0}.
\end{cases}\]取 $\overrightarrow n = \left(1,1,0\right)$，根据线面角的向量求法可得\[ \sin \theta = \left|\cos \left\langle \overrightarrow {BA} ,\overrightarrow n \right\rangle \right| = \left|\dfrac{{\overrightarrow {BA} \cdot \overrightarrow n}}{ { \left|\overrightarrow { BA} \right| \cdot \left|\overrightarrow n\right|}}\right| = \dfrac{2}{\sqrt 5 \times \sqrt 2 } = \dfrac{{\sqrt {10} }}{5}. \]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
