在直角坐标系 $xOy$ 中,已知点 $A\left( {1,1} \right)$,$B\left( {2,3} \right)$,$C\left( {3,2} \right)$,点 $P\left( {x,y} \right)$ 在 $\triangle ABC$ 三边围成的区域(含边界)上.
【难度】
【出处】
2014年高考陕西卷(理)
【标注】
-
若 $\overrightarrow {PA} + \overrightarrow {PB} + \overrightarrow {PC} = \overrightarrow 0 $,求 $\left| {\overrightarrow {OP} } \right|$;标注答案$ \left|\overrightarrow {OP} \right| = 2\sqrt 2 $.解析可先求得 $\overrightarrow {OP}$ 坐标,然后求 $\left|\overrightarrow {OP}\right|$.因为 $\overrightarrow {PA} + \overrightarrow {PB} + \overrightarrow {PC} = \overrightarrow 0 $,所以根据向量的加减法有\[\left(\overrightarrow {OA} - \overrightarrow {OP} \right) + \left(\overrightarrow {OB} - \overrightarrow {OP} \right) + \left(\overrightarrow {OC} - \overrightarrow {OP} \right) = \overrightarrow 0 ,\]即得 $\overrightarrow {OP} = \dfrac{1}{3}\left(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} \right) = \left(2,2\right)$,所以 $ \left|\overrightarrow {OP} \right| = 2\sqrt 2 $.
-
设 $\overrightarrow {OP} = m\overrightarrow {AB} + n\overrightarrow {AC}\left(m,n \in {\mathbb{R}}\right)$,用 $x$,$y$ 表示 $m - n$,并求 $m - n$ 的最大值.标注答案$ 1 $.解析利用条件 $\overrightarrow {OP} = m\overrightarrow {AB} + n\overrightarrow {AC} \left(m,n \in{\mathbb{ R}}\right)$ 得出 $x,y$ 和 $m,n$ 之间的关系,继而表示出 $m-n$,则问题转化成关于变量 $x,y$ 的线性规划问题.因为 $\overrightarrow {OP} = m\overrightarrow {AB} + n\overrightarrow {AC} $,所以根据平面向量的坐标运算得\[ \left(x,y\right) = \left(m + 2n,2m + n\right),\]即\[\begin{cases}
{x = m + 2n} ,\\
{y = 2m + n}.
\end{cases} \]两式相减得\[m - n = y - x.\]令 $y - x = t$,根据线性规划知识,由图可知,当直线 $y = x + t$ 过点 $B\left(2,3\right)$ 时,$t$ 取得最大值 $ 1 $,故 $m - n$ 的最大值为 $ 1 $.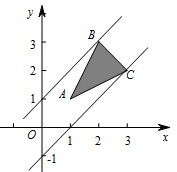
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2