如图,在平面四边形 $ABCD$ 中,$AD = 1$,$CD = 2$,$AC = \sqrt 7 $.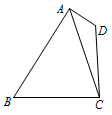

【难度】
【出处】
2014年高考湖南卷(理)
【标注】
-
求 $\cos \angle CAD$ 的值;标注答案$\dfrac{2\sqrt 7 }{7}$.解析本题考查余弦定理.在 $\triangle ADC$ 中,由余弦定理,得\[\cos \angle CAD = \dfrac{{A{C^2} + A{D^2} - C{D^2}}}{2AC \cdot AD}.\]故由题设知\[\cos \angle CAD = \dfrac{7 + 1 - 4}{2\sqrt 7 } = \dfrac{2\sqrt 7 }{7}. \]
-
若 $\cos \angle BAD = - \dfrac{\sqrt 7 }{14}$,$\sin \angle CBA = \dfrac{{\sqrt {21} }}{6}$,求 $BC$ 的长.标注答案$ 3$.解析$BC$ 在三角形 $ABC$ 中,同时三角形 $ABC$ 中已知 $AC$ 和其对角 $\angle ABC$,因此可以选择正弦定理或余弦定理求解 $BC$,若选择余弦定理,须知道 $AB$,题中条件不易求出 $AB$,因此需用正弦定理求解,那么求出 $\angle BAC$ 的正弦值是解题关键.设 $ \angle BAC=\alpha$,则 $\alpha=\angle BAD-\angle CAD $.
因为\[\cos \angle CAD= \dfrac{2\sqrt 7 }{7}, \cos \angle BAD = - \dfrac{\sqrt 7 }{14}\]所以\[\begin{split}\sin \angle CAD & \overset{\left[a\right]}=\sqrt{1-\cos^2\angle CAD}=\dfrac{\sqrt{21}}{7},\\ \sin \angle BAD & \overset{\left[a\right]}= \sqrt {1 - \cos ^2\angle BAD} = \dfrac{{3\sqrt {21} }}{14}.\end{split}\](推导中用到[a])
于是\[\begin{split}\sin \alpha & = \sin \left(\angle BAD - \angle CAD\right)
\\& \overset{\left[a\right]}= \sin \angle BAD\cos \angle CAD - \cos \angle BAD\sin \angle CAD
\\& = \dfrac{\sqrt 3 }{2}.\end{split}\](推导中用到[b])
在 $\triangle ABC$ 中,由正弦定理,得\[\dfrac{BC}{\sin \alpha} = \dfrac{AC}{\sin \angle CBA} ,\]代入数据,得 $BC=3$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2