如图，四棱柱 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 的所有棱长都相等，$AC \cap BD = O$，${A_1}{C_1} \cap {B_1}{D_1} = {O_1}$，四边形 $AC{C_1}{A_1}$ 和四边形 $BD{D_1}{B_1}$ 均为矩形．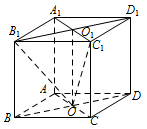
【难度】
【出处】
2014年高考湖南卷（理）
【标注】
-
证明：${O_1}O \perp 底面 ABCD$；标注答案略．解析在面上找两条相交直线均垂直于 $O_1O$ 即可．如图，因为四边形 $AC{C_1}{A_1}$ 为矩形，所以 $C{C_1} \perp AC$．
同理 $D{D_1} \perp BD$．
因为 $C{C_1} \parallel D{D_1}$，所以 $C{C_1} \perp BD$，而 $AC \cap BD = O$，因此 $C{C_1} \perp 底面 ABCD $．
由题设知，${O_1}O \parallel {C_1}C$，所以 ${O_1}O \perp 底面 ABCD $． -
若 $\angle CBA = 60^\circ $，求二面角 ${C_1} - O{B_1} - D$ 的余弦值．标注答案$\dfrac{{2\sqrt {57} }}{19}$．解析建立空间直角坐标系，求出两面的法向量，则法向量夹角的余弦值的绝对值与二面角的余弦值的绝对值相等，再判断二面角的锐钝即可．解法一：
如图，过 ${O_1}$ 作 ${O_1}H \perp O{B_1}$ 于 $ H $，连接 $H{C_1}$．
由（1）知，${O_1}O \perp 底面 ABCD $，所以 ${O_1}O \perp 底面 {A_1}{B_1}{C_1}{D_1}$，于是 ${O_1}O \perp {A_1}{C_1}$．
又因为四棱柱 $ABCD-{A_1}{B_1}{C_1}{D_1}$ 的所有棱长都相等，所以四边形 ${A_1}{B_1}{C_1}{D_1}$ 是菱形，因此 ${A_1}{C_1} \perp {B_1}{D_1}$．
从而 ${A_1}{C_1} \perp 平面 BD{D_1}{B_1}$，所以 ${A_1}{C_1} \perp O{B_1}$．
于是 $O{B_1} \perp 平面 {O_1}H{C_1}$，进而 $O{B_1} \perp {C_1}H$．
故 $\angle {C_1}H{O_1}$ 是二面角${C_1} - O{B_1} - D$ 的平面角．
不妨设 $ AB=2 $．因为 $\angle CBA = {60^\circ}$，所以\[OB = \sqrt 3 ,OC = 1,O{B_1} = \sqrt 7.\]在 ${\mathrm{Rt}}\triangle O{O_1}{B_1}$ 中，易知\[{O_1}H = \dfrac{{O{O_1} \cdot {O_1}{B_1}}}{{O{B_1}}} = 2\sqrt {\dfrac{3}{7}} .\]而 ${O_1}{C_1} = 1$，于是\[\begin{split}{C_1}H = \sqrt{{{O_1}{C_1}}^2 + {{O_1}H}^2} =\sqrt{\dfrac {19} 7 } .\end{split}\]所以\[\cos \angle {C_1}H{O_1} = \dfrac{{{O_1}H}}{{{C_1}H}} = \dfrac{{2\sqrt {57} }}{19},\]即二面角 ${C_1} - O{B_1} - D$ 的余弦值为 $\dfrac{{2\sqrt {57} }}{19}$．
解法二：
因为四棱柱 $ABCD-{A_1}{B_1}{C_1}{D_1}$ 的所有棱长都相等，所以四边形 $ ABCD $ 是菱形，因此 $AC \perp BD$．
又 ${O_1}O \perp 底面 ABCD $，从而 $OB$，$OC$，$ O{O_1}$ 两两垂直．
如图，以 $ O $ 为坐标原点，$OB$，$OC$，$O{O_1}$ 所在直线分别为 $ x $ 轴、$ y $ 轴、$ z $ 轴，建立空间直角坐标系．
不妨设 $ AB=2 $．因为 $\angle CBA = {60^\circ}$，所以\[OB = \sqrt 3 ,OC = 1,\]于是相关各点的坐标为\[ O\left(0,0,0\right) ,{B_1}\left(\sqrt 3 ,0,2\right),{C_1}\left(0,1,2\right).\]易知，$\overrightarrow {n_1} = \left(0,1,0\right)$ 是平面 $BD{D_1}{B_1}$ 的一个法向量．
设 $\overrightarrow {n_2} = \left(x,y,z\right)$ 是平面 $O{B_1}{C_1}$ 的一个法向量，则\[\begin{cases}
\overrightarrow {n_2} \cdot \overrightarrow {O{B_1}} = 0, \\
\overrightarrow {n_2} \cdot \overrightarrow {O{C_1}} = 0.\\
\end{cases}\]即\[\begin{cases}\sqrt 3 x + 2z = 0, \\
y + 2z = 0. \\
\end{cases}\]取 $z = - \sqrt 3 $，则 $x = 2$，$y = 2\sqrt 3 $，所以\[\overrightarrow {n_2} = \left(2,2\sqrt 3 , - \sqrt 3 \right).\]设二面角 ${C_1} - O{B_1} - D$ 的大小为 $\theta $，易知 $\theta $ 是锐角，于是\[ \cos \theta = \left| {\cos \left\langle \overrightarrow {n_1},\overrightarrow {n_2} \right\rangle } \right| = \left| {\dfrac{{\overrightarrow{n_1} \cdot \overrightarrow{n_2}}}{{\left| {\overrightarrow{n_1}} \right| \cdot \left| {\overrightarrow{n_2}} \right|}}} \right| = \dfrac{{2\sqrt {57} }}{19}. \]故二面角 ${C_1} - O{B_1} - D$ 的余弦值为 $\dfrac{{2\sqrt {57} }}{19}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
