一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.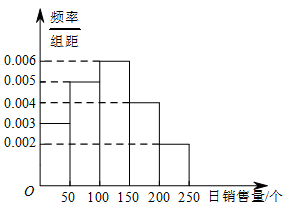

【难度】
【出处】
2014年高考辽宁卷(理)
【标注】
-
求在未来连续 $ 3 $ 天里,有连续 $ 2 $ 天的日销售量都不低于 $ 100 $ 个且另 $ 1 $ 天的日销售量低于 $ 50 $ 个的概率;标注答案$ 0.108$解析先结合频率分布直方图得到各个销售量段内的概率,然后再根据概率的公式计算.设 ${A_1}$ 表示事件“日销售量不低于 $ 100 $ 个”,${A_2}$ 表示事件“日销售量低于 $ 50 $ 个”,$ B $ 表示事件“在未来连续 $ 3 $ 天里有连续 $ 2 $ 天日销售量不低于 $ 100 $ 个且另 $ 1 $ 天的日销售量低于 $ 50 $ 个”.因此\[\begin{split}P\left({A_1}\right) &\overset{\left[a\right]}= \left(0.006 + 0.004 + 0.002\right) \times 50 = 0.6,\\P\left({A_2}\right) &\overset{\left[b\right]}= 0.003 \times 50 = 0.15,\\P\left(B\right) &\overset{\left[c\right]}= 0.6 \times 0.6 \times 0.15 \times 2 = 0.108.\end{split}\](推导中用到:[a][b][c])
-
用 $X$ 表示在未来 $ 3 $ 天里日销售量不低于 $ 100 $ 个的天数,求随机变量 $X$ 的分布列,期望 $E\left( X \right)$ 及方差 $D\left( X \right)$.标注答案分布列为
$\begin{array}{|c|c|c|c|c|} \hline
X&0&1&2&3 \\ \hline
P&0.064&0.288&0.432&0.216 \\ \hline
\end{array}$
期望 $E\left(X\right)=1.8 $,方差 $D\left(X\right)=0.72 $.解析本题是独立重复试验模型,考查二项分布的分布列和数学期望.$ X $ 的可能取值为 $ 0,1,2,3 $,相应的概率为\[\begin{split}P\left(X = 0\right) &= {\mathrm{C}}_3^0 \cdot {\left(1 - 0.6\right)^3} = 0.064,\\P\left(X = 1\right) &={\mathrm{ C}}_3^1 \cdot 0.6{\left(1 - 0.6\right)^2} = 0.288,\\P\left(X = 2\right) &= {\mathrm{C}}_3^2 \cdot {0.6^2}\left(1 - 0.6\right) = 0.432,\\P\left(X = 3\right) &= {\mathrm{C}}_3^3 \cdot {0.6^3} = 0.216,\end{split}\]分布列为\[\begin{array}{|c|c|c|c|c|} \hline
X&0&1&2&3 \\ \hline
P&0.064&0.288&0.432&0.216 \\ \hline
\end{array}\]因为 $X\sim B\left(3,0.6\right) $,所以期望为\[E\left(X\right)=3\times 0.6=1.8 ,\]方差\[D\left(X\right)=3\times 0.6\times \left(1-0.6\right)=0.72. \]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2