如图，$\triangle ABC$ 和 $\triangle BCD$ 所在平面互相垂直，且 $AB = BC = BD = 2$，$\angle ABC = \angle DBC = 120^\circ $，$E$，$F$ 分别为 $AC$，$DC$ 的中点．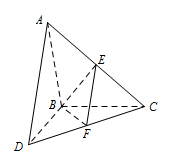
【难度】
【出处】
2014年高考辽宁卷（理）
【标注】
-
求证：$EF \perp BC$；标注答案略解析要借助面面垂直和边的关系来证明，注意辅助线的构造．法一：
过 $ E $ 作 $ EO\perp BC $，垂足为 $ O $，连 $ OF $，如图，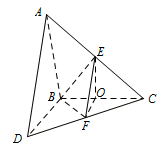
由 $ \triangle ABC\cong \triangle DBC $ 可证出 $ \triangle EOC\cong \triangle FOC $，
所以 $\angle EOC=\angle FOC= \dfrac{{\mathrm \pi} }{2}$，即 $ FO\perp BC $．
又 $ EO\perp BC $，因此 $ BC\perp $ 面 $ EFO $，
又 $ EF \subset $ 面 $ EFO $，所以 $ EF\perp BC$．
法二：
由题意，以 $ B $ 为坐标原点，在平面 $ DBC $ 内过 $ B $ 作垂直 $ BC $ 的直线为 $ x $ 轴，$ BC $ 所在直线为 $ y $ 轴，在平面 $ ABC $ 内过 $ B $ 作垂直 $ BC $ 的直线为 $ z $ 轴，建立如图所示的空间直角坐标系．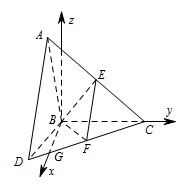
易得\[ B\left(0,0,0\right),A\left(0,-1, \sqrt 3 \right),D\left( \sqrt 3 ,-1,0\right),C\left(0,2,0\right) ,\]因而\[E\left(0,\dfrac{1}{2},\dfrac{\sqrt 3 }{2}\right),F\left(\dfrac{\sqrt 3 }{2},\dfrac{1}{2},0\right),\]所以\[\overrightarrow {EF} = \left(\dfrac{\sqrt 3 }{2},0, - \dfrac{\sqrt 3 }{2}\right), \overrightarrow {BC} = \left(0,2,0\right),\]因此 $\overrightarrow {EF} \cdot \overrightarrow {BC} = 0$，从而 $\overrightarrow {EF} \perp \overrightarrow {BC} $，所以 $EF \perp BC$． -
求二面角 $E - BF - C$ 的正弦值标注答案$\dfrac{2\sqrt 5 }{5}$．解析在第一问的基础上，利用三垂线定理构造二面角．法一：
过 $ O $ 作 $ OG\perp BF $，垂足为 $ G $，连 $ EG $，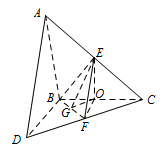
由平面 $ ABC\perp $ 平面 $ BDC $，得 $ EO\perp $ 平面 $ BDC $，所以 $EO\perp BF$．
又 $ OG\perp BF $，所以 $BF\perp$ 平面 $EOG$，从而 $ EG \perp BF $．
因此 $ \angle EGO $ 为二面角 $ E-BF-C $ 的平面角；
在 $ \triangle EOC $ 中，可得\[EO= \dfrac{1}{2}EC= \dfrac{1}{2} BC\cdot \cos 30^\circ = \dfrac{\sqrt 3 }{2} ,\]由 $ \triangle BGO\backsim \triangle BFC $知\[OG = \dfrac{BO}{BC} \cdot FC = \dfrac{\sqrt 3 }{4},\]因此\[\tan \angle EGO= \dfrac{EO}{OG} = 2,\]从而\[\sin \angle EGO= \dfrac{2\sqrt 5 }{5},\]即二面角 $ E-BF-C $ 的正弦值为 $\dfrac{2\sqrt 5 }{5}$．
法二：
在图中，平面 $ BFC $ 的一个法向量为 $\overrightarrow {n_1} = \left(0,0,1\right)$，设平面 $ BEF $ 的法向量$\overrightarrow {n_2} = \left(x,y,z\right)$，又\[\overrightarrow {BF} = \left(\dfrac{\sqrt 3 }{2},\dfrac{1}{2},0\right), \overrightarrow {BE} = \left(0,\dfrac{1}{2},\dfrac{\sqrt 3 }{2}\right),\]由\[\begin{cases}
\overrightarrow {n_2} \cdot \overrightarrow {BF} = 0, \\
\overrightarrow {n_2} \cdot \overrightarrow {BE} = 0, \\
\end{cases}\]得其中一个法向量为\[\overrightarrow {n_2} = \left(1, - \sqrt 3 ,1\right),\]设二面角 $ E-BF-C $ 的大小为 $\theta $，且由题意知 $\theta $ 为锐角，则\[\cos \theta = \left |\cos \left\langle \overrightarrow {n_1} ,\overrightarrow {n_2} \right\rangle \right | = \left |\dfrac{{\overrightarrow {n_1} \cdot \overrightarrow {n_2} }}{{ \left|\overrightarrow {n_1} \right| \cdot {\left|{\overrightarrow {n_2} }\right|}}} \right| = \dfrac{1}{\sqrt 5 },\]所以\[\sin \theta = \dfrac{2}{\sqrt 5 } = \dfrac{2\sqrt 5 }{5},\]即二面角 $ E-BF-C $ 的正弦值为 $\dfrac{2\sqrt 5 }{5}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
