如图,$ EP $ 交圆于 $ E$,$C $ 两点,$ PD $ 切圆于 $ D $,$ G $ 为 $ CE $ 上一点且 $PG = PD$,连接 $ DG $ 并延长交圆于点 $ A $,作弦 $ AB $ 垂直 $ EP $,垂足为 $ F $.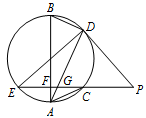

【难度】
【出处】
2014年高考辽宁卷(理)
【标注】
-
求证:$ AB $ 为圆的直径;标注答案略解析本题考查圆的切线的相关知识.因为 $PG = PD$,所以 $\angle PDG = \angle PGD$.
由于 $PD$ 为切线,所以 $\angle PDA = \angle DBA$,
又由于 $\angle PGD = \angle EGA$,则 $\angle DBA = \angle EGA$,
所以 $\angle DBA + \angle BAD = \angle EGA + \angle BAD$,
从而 $\angle BDA = \angle PFA$,
由于 $AF \perp EP$,即 $\angle PFA = {90^\circ}$,
于是 $\angle BDA = {90^\circ}$,故 $AB$ 为圆的直径. -
若 $ AC=BD $,求证:$ AB=ED $.标注答案略解析本题考查圆的相关性质.连接 $BC$,$DC$.由于 $AB$ 是直径,故 $\angle BDA = \angle ACB = {90^\circ}$.
在 ${\mathrm{Rt}}\triangle BDA$ 和 ${\mathrm{Rt}}\triangle ACB$ 中,$AB = BA$,$AC = BD$,
从而 ${\mathrm{Rt}}\triangle BDA \cong {\mathrm{Rt}}\triangle ACB$,于是 $\angle DAB = \angle CBA$,
又因为 $\angle DCB = \angle DAB$,所以 $\angle DCB = \angle CBA$,于是 $DC\parallel AB$.
由于 $AB \perp EP$,所以 $DC \perp EP$,于是 $ED$ 为直径,由(1)得,$ED = AB$.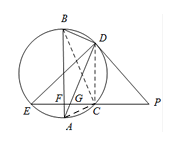
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2