如图，在棱长为 $2$ 的正方体 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 中，$E$，$F$，$M$，$N$ 分别是棱 $AB$，$AD$，${A_1}{B_1}$，${A_1}{D_1}$ 的中点，点 $P$，$Q$ 分别在棱 $D{D_1}$，$B{B_1}$ 上移动，且 $DP = BQ = \lambda \left(0 < \lambda < 2 \right) $．
【难度】
【出处】
2014年高考湖北卷（理）
【标注】
-
当 $\lambda = 1$ 时，证明：直线 $B{C_1}\parallel $ 平面 $EFPQ$；标注答案略解析本题需要以 $AD_1$ 作为过渡．方法一：
如图，连接 $A{D_1}$，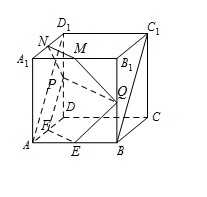
由 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 是正方体，知 $B{C_1}\parallel A{D_1}$，当 $\lambda = 1$ 时，$P$ 是 $D{D_1}$ 的中点．
又 $F$ 是 $AD$ 的中点，所以 $FP\parallel A{D_1}$，所以 $B{C_1}\parallel FP$，而 $FP \subset $ 平面 $EFPQ$，且 $B{C_1} \not\subset $ 平面 $EFPQ$，故直线 $B{C_1}\parallel $ 平面 $EFPQ$．
方法二：
以 $D$ 为原点，射线 $DA$，$DC$，$D{D_1}$ 分别为 $x,y,z$ 轴的正半轴建立如图的空间直角坐标系 $D - xyz$．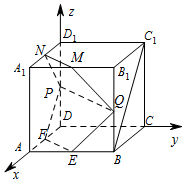
由已知得 $B\left(2,2,0\right)$，${C_1}\left(0,2,2\right)$，$F\left(1,0,0\right)$，$P\left(0,0,\lambda \right)$，$E\left(2,1,0\right)$，所以\[\overrightarrow {B{C_1}} = \left( - 2,0,2\right), \overrightarrow {FP} = \left( - 1,0,\lambda \right),
\overrightarrow {FE} = \left(1,1,0\right),\]当 $\lambda = 1$ 时，$\overrightarrow {FP} = \left( - 1,0,1\right)$，因为 $\overrightarrow {B{C_1}} = \left( - 2,0,2\right)$，所以\[\overrightarrow {B{C_1}} = 2\overrightarrow {FP} ,\]即 $B{C_1}\parallel FP$，而 $FP \subset $ 平面 $EFPQ$，且 $B{C_1} \not\subset $ 平面 $EFPQ$，故直线 $B{C_1}\parallel $ 平面 $EFPQ$． -
是否存在 $\lambda $，使平面 $EFPQ$ 与面 $PQMN$ 所成的二面角为直二面角？若存在，求出 $\lambda $ 的值；若不存在，说明理由．标注答案$\lambda = 1 \pm \dfrac{\sqrt 2 }{2}$解析本题需要先构造出二面角，然后利用边的关系构建方程，最后求出未知数；也可以用向量来解决．方法一：
如图，连接 $BD$．
因为 $E$，$F$ 分别是 $AB$，$AD$ 的中点，所以 $EF\parallel BD$，且\[EF = \dfrac{1}{2}BD,\]又 $DP = BQ$，$DP\parallel BQ$，所以四边形 $PQBD$ 是平行四边形，故 $PQ\parallel BD$，且 $PQ = BD$，从而 $EF\parallel PQ$，且\[EF = \dfrac{1}{2}PQ.\]在 ${\mathrm{Rt}}\triangle EBQ$ 和 ${\mathrm{Rt}}\triangle FDP$ 中，因为\[BQ = DP = \lambda , BE = DF = 1,\]于是\[EQ = FP = \sqrt {1 + {\lambda ^2}} ,\]所以四边形 $EFPQ$ 是等腰梯形．
同理可证四边形 $PQMN$ 是等腰梯形．
分别取 $EF$，$PQ$，$MN$ 的中点为 $H$，$O$，$G$，连接 $OH$，$OG$，则 $GO \perp PQ$，$HO \perp PQ$，而 $GO \cap HO = O$，故 $\angle GOH$ 是平面 $EFPQ$ 与平面 $PQMN$ 所成的二面角的平面角．
若存在 $\lambda $，使平面 $EFPQ$ 与平面 $PQMN$ 所成的二面角为直二面角，则\[\angle GOH = {90^ \circ },\]连接 $EM$，$FN$，则由 $EF\parallel MN$，且 $EF = MN$，知四边形 $EFNM$ 是平行四边形．
连接 $GH$，因为 $H$，$G$ 是 $EF$，$MN$ 的中点，所以\[GH = ME = 2.\]在 $\triangle GOH$ 中，则\[\begin{split}G{H^2} & = 4, \\ O{H^2} & = 1 + {\lambda ^2} - {\left(\dfrac{\sqrt 2 }{2}\right)^2} = {\lambda ^2} + \dfrac{1}{2} , \\ O{G^2} & = 1 + {\left(2 - \lambda \right)^2} - {\left(\dfrac{\sqrt 2 }{2}\right)^2} = {\left(2 - \lambda \right)^2} + \dfrac{1}{2},\end{split}\]由 $O{G^2} + O{H^2} = G{H^2}$ 得\[{\left(2 - \lambda \right)^2} + \dfrac{1}{2} + {\lambda ^2} + \dfrac{1}{2} = 4,\]解得 $\lambda = 1 \pm \dfrac{\sqrt 2 }{2}$，故当 $\lambda = 1 \pm \dfrac{\sqrt 2 }{2}$ 时，平面 $EFPQ$ 与平面 $PQMN$ 所成的二面角为直二面角．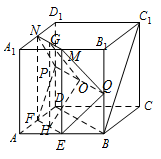
方法二：
设平面 $EFPQ$ 的一个法向量${\overrightarrow{n}} = \left(x,y,z\right)$，由\[ \begin{cases}
\overrightarrow {FE} \cdot {\overrightarrow{n}} = 0, \\
\overrightarrow {FP} \cdot {\overrightarrow{n}} = 0, \\
\end{cases} \]可得\[\begin{cases}x + y = 0 ,\\
- x + \lambda z = 0 ,\\
\end{cases}\]于是可取 ${\overrightarrow{n}} = \left(\lambda , - \lambda ,1\right)$．
同理可得平面 $MNPQ$ 的一个法向量为 ${\overrightarrow{m}} = \left(\lambda - 2,2 - \lambda ,1\right)$．
若存在 $\lambda $，使平面 $EFPQ$ 与平面 $PQMN$ 所成的二面角为直二面角，则\[{\overrightarrow{m}} \cdot {\overrightarrow{n}} = \left(\lambda - 2,2 - \lambda ,1\right) \cdot \left(\lambda , - \lambda ,1\right) = 0,\]即\[\lambda \left(\lambda - 2\right) - \lambda \left(2 - \lambda \right) + 1 = 0,\]解得 $\lambda = 1 \pm \dfrac{\sqrt 2 }{2}$，故当 $\lambda = 1 \pm \dfrac{\sqrt 2 }{2}$ 时，平面 $EFPQ$ 与平面 $PQMN$ 所成的二面角为直二面角．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
