如图，在四棱锥 $A - BCDE$ 中，$平面 ABC \perp 平面 BCDE$，$\angle CDE = \angle BED = 90^\circ $，$AB = CD = 2$，$DE = BE = 1$，$AC = \sqrt 2 $．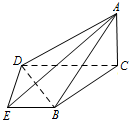
【难度】
【出处】
2014年高考浙江卷（理）
【标注】
-
证明：$DE \perp 平面 ACD$；标注答案略解析本题证明垂直时注意利用面面垂直的条件和边的关系．取 $CD$ 中点 $F$，连接 $BF$，则 $DF=\dfrac{1}{2}CD=1 $．
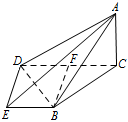因为 $\angle CDE = \angle BED = 90^\circ $，$ DE=BE=DF=1$，所以四边形 $BFDE$ 为正方形，所以\[BD=BC=\sqrt 2. \]由 $ AC=\sqrt 2 $，$AB=2$，得\[ {AB}^2={AC}^2+{BC}^2,\]即 $AC\perp BC $．
又因为 $平面ABC \perp 平面 BCDE$，$平面ABC \cap 平面 BCDE=BC $，所以 $AC \perp 平面 BCDE$，所以 $AC \perp DE$．
又 $DE \perp CD$，$ AC\cap CD=C $，所以 $DE \perp 平面 ACD$． -
求二面角 $B - AD - E$ 的大小．标注答案$\dfrac{\mathrm \pi} {6}$．解析本题用空间向量求解二面角即可．以 $ D $ 为原点，分别以射线 $ DE$，$DC $ 为 $ x$，$y $ 轴的正半轴，建立空间直角坐标系 $ D-xyz $ 如图所示，
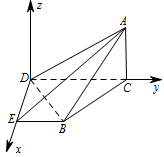由题意可知，各点的坐标如下：\[D\left(0,0,0\right) , E\left(1,0,0\right) , B\left(1,1,0\right) , C\left(0,2,0\right) , A\left(0,2,\sqrt 2 \right) .\]设平面 $ ADE$ 的法向量是 $\overrightarrow {n_1}= \left({x_1},{y_1},{z_1}\right)$，平面 $ABD$ 的法向量是 $\overrightarrow {n_2} =\left({x_2},{y_2},{z_2}\right)$，则\[ \begin{cases} {\overrightarrow {DE} \cdot \overrightarrow {n_1} = 0}, \\
{\overrightarrow {DA} \cdot \overrightarrow {n_1} = 0}
.\end{cases} \]即\[ {\begin{cases}{x_1} = 0, \\
2{y_1} + \sqrt 2 {z_1} = 0, \\
\end{cases}}\]令 $y_1=1$，可得 $\overrightarrow {n_1} =\left(0,1, - \sqrt 2 \right)$，同理\[\begin{cases}\overrightarrow {DB} \cdot \overrightarrow {n_2} = 0 ,\\
\overrightarrow {DA} \cdot \overrightarrow {n_2} = 0 .\\
\end{cases}\]即\[ {\begin{cases}{x_2} + {y_2} = 0 ,\\
2{y_2} + \sqrt 2 {z_2} = 0 ,\\
\end{cases}}\]令 $y_2=1$，可得 $\overrightarrow {n_2} = \left( - 1,1, - \sqrt 2 \right)$．
设二面角 $B - AD - E$ 的平面角为 $\theta $，由图知 $\theta $ 为锐角，则\[\cos \theta = \left| {\left. {\dfrac{{\overrightarrow {n_1} \cdot \overrightarrow {n_2} }}{{\left| {\overrightarrow {n_1} } \right| \cdot \left| {\overrightarrow {n_2} } \right|}}} \right|} \right. = \dfrac{1 + 2}{{\sqrt {1 + 2} \cdot \sqrt {1 + 1 + 2} }} = \dfrac{\sqrt 3 }{2},\]即二面角 $B - AD - E$ 的大小是 $\dfrac{\mathrm \pi} {6}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
