从某企业生产的某种产品中抽取 $ 500 $ 件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图: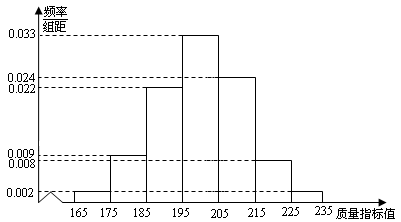

【难度】
【出处】
2014年高考新课标Ⅰ卷(理)
【标注】
-
求这 $ 500 $ 件产品质量指标值的样本平均数 $\overline x $ 和样本方差 ${s^2}$(同一组中的数据用该组区间的中点值作代表);标注答案$ \overline x= 200 $;$ s^2= 150 $解析本题考查频率分布直方图、平均数以及方差的相关知识.频率分布直方图中的每一组在计算平均数时,取中间值计算.由频率分布直方图可得,抽取产品的质量指标值的样本平均数\[\begin{split}\overline x &= 170 \times 0.02 + 180 \times 0.09 + 190 \times 0.22 + 200 \times 0.33 + 210 \times 0.24 + 220 \times 0.08 + 230 \times 0.02 \\&= 200,\end{split} \]样本方差\[\begin{split} s^2 & = \left( - 30 \right)^2 \times 0.02 + \left( - 20 \right)^2 \times 0.09 + \left( - 10 \right)^2 \times 0.22 + 0 \times 0.33 + {10^2} \times 0.24 + {20^2} \times 0.08 + {30^2} \times 0.02 \\& = 150.\end{split}\]
-
由直方图可以认为,这种产品的质量指标值 $Z$ 服从正态分布 $N\left(\mu ,{\sigma ^2}\right)$,其中 $\mu $ 近似为样本平均数 $\overline x $,${\sigma ^2}$ 近似为样本方差 ${s^2}$.
(i)利用该正态分布,求 $P\left(187.8 < Z < 212.2\right)$;
(ii)某用户从该企业购买了 $ 100 $ 件这种产品,记 $X$ 表示这 $ 100 $ 件产品中质量指标值位于区间 $\left( {187.8,212.2} \right)$ 的产品件数,利用(i)的结果,求 $EX$.
附:$\sqrt {150} \approx 12.2$,若 $Z \sim N\left(\mu ,{\sigma ^2}\right)$,则 $P\left(\mu - \sigma < Z < \mu + \sigma \right) = 0.6826$,$P\left(\mu - 2\sigma < Z < \mu + 2\sigma \right) = 0.9544$.标注答案(i)$ P\left( {187.8 < Z < 212.2} \right) = 0.6826 $;(ii)$ EX = 68.26 $.解析本题考查正态分布、二项分布相关问题.(i)由(1)知,$Z \sim N \left( {200,150} \right)$,从而\[\begin{split}P\left( {187.8 < Z < 212.2} \right) & = P\left( {200 - 12.2 < Z < 200 + 12.2} \right) \\& = 0.6826.\end{split}\](ii)由(i)知,一件产品的质量指标值位于区间 $\left( {187.8,212.2} \right)$ 的概率为 $0.6826$,
依题意知 $X \sim B\left( {100,0.6826} \right)$,所以\[EX = 100 \times 0.6826 = 68.26.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2