如图，四边形 $ABCD$ 是 $ \odot O$ 的内接四边形，$AB$ 的延长线与 $DC$ 的延长线交于点 $E$，且 $CB = CE$．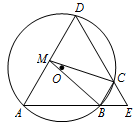
【难度】
【出处】
2014年高考新课标Ⅰ卷（理）
【标注】
-
证明：$\angle D = \angle E$；标注答案略解析本题考查圆内接四边形的性质．由题设得，$A,B,C,D$ 四点共圆，所以 $\angle D = \angle CBE$．
由已知 $CB=CE$，得 $\angle CBE = \angle E$，
所以 $\angle D = \angle E$． -
设 $AD$ 不是 $ \odot O$ 的直径，$AD$ 的中点为 $M$，且 $MB = MC$，证明：$\triangle ADE$ 为等边三角形．标注答案略解析本题考查垂径定理相关应用．如图，
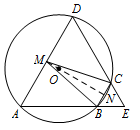设 $BC$ 中点为 $N$，连接 $MN$．
由 $MB = MC$，知 $MN \perp BC$，
所以 $O$ 在 $MN$ 上．
又 $AD$ 不是 $ \odot O$ 的直径，$M$ 为 $AD$ 中点，
故 $OM \perp AD$，即 $MN \perp AD$，
所以 $AD \parallel BC$，
故 $\angle A = \angle CBE$．
又 $\angle CBE = \angle E$，
故 $\angle A = \angle E$．
由（1）知，$\angle D = \angle E$，所以 $\triangle ADE$ 为等边三角形．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
