题目 随机观测生产某种零件的某工厂 $ 25 $ 名工人的日加工零件数（单位：件），获得数据如下：$30$，$42$，$41$，$36$，$44$，$40$，$37$，$37$，$25$，$45$，$29$，$43$，$31$，$36$，$49$，$34$，$33$，$43$，$38$，$42$，$32$，$34$，$46$，$39$，$36$．<br/>根据上述数据得到样本的频率分布表如下：\[\begin{array} {ccc} \\ \hline<br/>分组 & 频数 & 频率 \\ \hline<br/>\left[25,30\right] & 3 & 0.12 \\<br/>\left(30,35\right] & 5 & 0.20 \\<br/>\left(35,40\right] & 8 & 0.32 \\<br/>\left(40,45\right] & {n_1} & {f_1} \\<br/>\left(45,50\right] & {n_2} & {f_2} \\ \hline \end{array}\] 问题1 确定样本频率分布表中 ${n_1}$，${n_2}$，${f_1}$ 和 ${f_2}$ 的值； 答案1 ${n_1} = 7$，${n_2} = 2$，${f_1} = 0.28$，${f_2} = 0.08$． 解析1 本题考查的是频率与频数，属于基础题．从获得的 $25$ 名工人的样本数据可知 ${n_1} = 7$，${n_2} = 2$．所以加工零件数在 $\left(40,45\right]$ 的频率是 ${f_1} =\dfrac{7}{25} =0.28$，加工零件数在 $\left(45,50\right]$ 的频率是 ${f_2} =\dfrac{2}{25}= 0.08$． 备注1 问题2 根据上述频率分布表，画出样本频率分布直方图； 答案2 解析2 本题考查的是画频率直方图，基础题．根据上述频率分布表，样本的频率分布直方图如下：<img src="/static/images/0a5aed9ba23bf78750d9dea04b190f17.jpg" class="img-responsive" /> 备注2 问题3 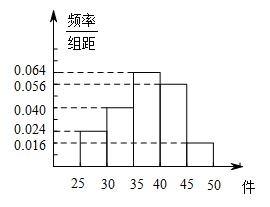根据样本频率分布直方图，求在该厂任取 $4$ 人，至少有 $1$ 人的日加工零件数落在区间 $ \left(30,35\right] $ 的概率． 答案3 至少有 $ 1 $ 人的日加工零件数落在区间 $ \left(30,35\right] $ 的概率为 $ 0.5904 $． 解析3 本小题考查的是二项分布．根据样本频率分布直方图，每人的日加工零件数落在区间 $ \left(30,35\right] $ 的概率为 $ 0.2 $，设所取的 $ 4 $ 人中，日加工零件数落在区间 $ \left(30,35\right] $ 的人数为 $\xi$，则 $\xi \sim B\left(4,0.2\right) $，\[\begin{split}P\left(\xi \geqslant 1\right) &= 1- P\left(\xi =0\right) \\&= 1 - \left(1-0.2\right)^4 \\&= 0.5904,\end{split}\]所以 $ 4 $ 人中，至少有 $ 1 $ 人的日加工零件数落在区间 $ \left(30,35\right] $ 的概率为 $ 0.5904 $． 备注3