如图，在四棱柱 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 中，底面 $ABCD$ 是等腰梯形，$\angle DAB = {60^ \circ }$，$AB = 2CD = 2$，$M$ 是线段 $AB$ 的中点．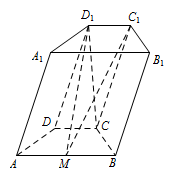
【难度】
【出处】
2014年高考山东卷（理）
【标注】
-
求证：${C_1}M \parallel 平面{A_1}AD{D_1}$；标注答案略．解析本小问考查了线面平行的证明，线面平行一般通过构造平行四边形，中位线，或构造平行平面的方法来证．因为四边形 $ABCD$ 是等腰梯形，且 $AB = 2CD$，所以 $AB \parallel DC $．
又由 $M$ 是 $AB$ 中点，因此 $CD \parallel MA$ 且 $CD = MA$．
连接 $A{D_1}$，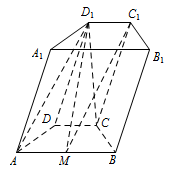
在四棱柱 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 中，因为 $CD \parallel {C_1}{D_1}$，$CD = {C_1}{D_1}$，可得 ${C_1}{D_1} \parallel MA$，${C_1}{D_1} = MA$，所以四边形 $AM{C_1}{D_1}$ 为平行四边形，因此 ${C_1}M \parallel {D_1}A$．
又 ${C_1}M \not\subset $ 平面 ${A_1}AD{D_1}$，${D_1}A \subset $ 平面 ${A_1}AD{D_1}$，所以 ${C_1}M \parallel $ 平面 ${A_1}AD{D_1}$． -
若 $C{D_1}$ 垂直于平面 $ABCD$ 且 $C{D_1} = \sqrt 3 $，求平面 ${C_1}{D_1}M$ 和平面 $ABCD$ 所成的角（锐角）的余弦值．标注答案$\dfrac{\sqrt 5}{5}$．解析本小题考查了求二面角．根据已知条件可以作出二面角，然后利用余弦定理解三角形，求得二面角的平面角的余弦值．由（1）知，平面 ${D_1}{C_1}M \cap $ 平面 $ABCD = AB$．过 $C$ 向 $AB$ 作垂线交 $AB$ 于 $N$，连接 ${D_1}N$．
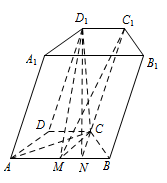由 $C{D_1} \perp 面ABCD$，可得 ${D_1}N \perp AB$，故 $\angle {D_1}NC$ 为二面角 ${C_1} - AB - C$ 的平面角．
在 ${\mathrm{Rt}} \triangle {D_1}CN$ 中，$BC = 1$，$\angle NBC = 60^\circ$，可得 $CN = \dfrac{\sqrt 3 }{2}$，所以\[N{D_1} = \sqrt {CD_1^2 + C{N^2}} = \dfrac{{\sqrt {15} }}{2}.\]在 ${\mathrm{Rt}}\triangle {D_1}CN$ 中，\[\cos \angle {D_1}NC = \dfrac{CN}{{{D_1}N}} = \dfrac{{\dfrac{\sqrt 3 }{2}}}{{\dfrac{{\sqrt {15} }}{2}}} = \dfrac{\sqrt 5 }{5},\]所以平面 ${C_1}{D_1}M$ 和平面 $ABCD$ 所成的角（锐角）的余弦值为 $\dfrac{\sqrt 5 }{5}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
