乒乓球台面被球网分隔成甲、乙两部分,如图,甲上有两个不相交的区域 $ A $,$ B $,乙被划分为两个不相交的区域 $ C $,$ D $.某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在 $ C $ 上记 $ 3 $ 分,在 $ D $ 上记 $ 1 $ 分,其他情况记 $ 0 $ 分.对落点在 $ A $ 上的来球,队员小明回球的落点在 $ C $ 上的概率为 $\dfrac{1}{2}$,在 $ D $ 上的概率为 $\dfrac{1}{3}$;对落点在 $ B $ 上的来球,小明回球的落点在 $ C $ 上的概率为 $\dfrac{1}{5}$,在 $ D $ 上的概率为 $\dfrac{3}{5}$.假设共有两次来球且落在 $ A $,$ B $ 上各一次,小明的两次回球互不影响.求: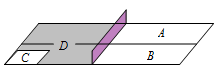

【难度】
【出处】
2014年高考山东卷(理)
【标注】
-
小明两次回球的落点中恰有一次的落点在乙上的概率;标注答案$\dfrac{3}{10}$.解析小明回球落在乙上的概率与来球落得位置有关,故需要把事件“恰有一次落在乙上”的所有情况都写出,这些事件都是互斥事件.设 $E$ 为事件“来球落在 $A$ 上,回球落在乙上”,则\[P\left(E\right)\overset{\left[a\right]}=\dfrac{1}{2}+\dfrac{1}{3}=\dfrac{5}{6}.\](推导中用到:[a])
设 $F$ 为事件“来球落在 $B$ 上,回球落在乙上”,则\[P\left(F\right)\overset{\left[a\right]}=\dfrac{1}{5}+\dfrac{3}{5}=\dfrac{4}{5}.\](推导中用到:)
设回球的落点恰有一次在乙上为事件 $G$,则\[P\left(G \right) \overset{\left[b\right]}= P\left(E\right)\cdot P\left(\overline F\right)+P\left(\overline E\right)\cdot P\left(F\right)=\dfrac{5}{6} \times \dfrac{1}{5} + \dfrac{1}{6} \times \dfrac{4}{5} = \dfrac{3}{10}.\](推导中用到:[b]) -
两次回球结束后,小明得分之和 $\xi $ 的分布列与数学期望.标注答案$ \xi $ 的分布列为:\[\begin{array}{|c|c|c|c|c|c|c|} \hline \xi & 0 & 1 & 2 & 3 & 4 & 6 \\ \hline P & \frac{1}{30} & \frac 1 6 & \frac 1 5 & \frac{2}{15} & \frac{11}{30} & \frac{1}{10} \\ \hline \end{array}\]数学期望为 $E\left( \xi \right) = \dfrac{91}{30}$.解析考查离散型随机变量的分布列与数字特征,根据题目条件,将独立事件的概率计算出来即可.$\xi $ 的可能取值为 $0$,$ 1 $,$ 2 $,$ 3 $,$ 4 $,$6$.
由事件的独立性与互斥性可得\[\begin{split}P\left( {\xi = 0} \right) & = \dfrac{1}{6} \times \dfrac{1}{5} = \dfrac{1}{30} ,\\ P\left( {\xi = 1} \right) & = \dfrac{1}{3} \times \dfrac{1}{5} + \dfrac{1}{6} \times \dfrac{3}{5} = \dfrac{1}{6} ,\\ P\left( {\xi = 2} \right) & = \dfrac{1}{3} \times \dfrac{3}{5} = \dfrac{1}{5}, \\ P\left( {\xi = 3} \right) & = \dfrac{1}{2} \times \dfrac{1}{5} + \dfrac{1}{6} \times \dfrac{1}{5} = \dfrac{2}{15} , \\ P\left( {\xi = 4} \right) & = \dfrac{1}{2} \times \dfrac{3}{5} + \dfrac{1}{3} \times \dfrac{1}{5} = \dfrac{11}{30}, \\ P\left( {\xi = 6} \right) & = \dfrac{1}{2} \times \dfrac{1}{5} = \dfrac{1}{10}.\end{split}\]所以 $ \xi $ 的分布列为:\[\begin{array}{|c|c|c|c|c|c|c|} \hline \xi & 0 & 1 & 2 & 3 & 4 & 6 \\ \hline P & \frac{1}{30} & \frac 1 6 & \frac 1 5 & \frac{2}{15} & \frac{11}{30} & \frac{1}{10} \\ \hline \end{array}\]所以其数学期望为\[\begin{split}E\left( \xi \right) & = 0 \times \dfrac{1}{30} + 1 \times \dfrac{1}{6} + 2 \times \dfrac{1}{5} + 3 \times \dfrac{2}{15} + 4 \times \dfrac{11}{30} + 6 \times \dfrac{1}{10} \\& = \dfrac{91}{30}.\end{split}\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2