如图,在 $\triangle ABC$ 中,$\angle B = \dfrac{{\mathrm{\mathrm \pi} } }{3}$,$AB = 8$,点 $D$ 在 $BC$ 边上,且 $CD = 2$,$\cos \angle ADC = \dfrac{1}{7}$.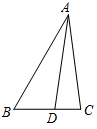
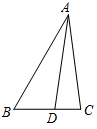
【难度】
【出处】
2014年高考北京卷(理)
【标注】
-
求 $\sin \angle BAD$;标注答案$ \dfrac{3\sqrt 3 }{14} $解析注意到所求角与已知角的关系,构造差角形式,利用公式进行求解.因为\[\sin \angle ADC \overset{\left[a\right]}= \sqrt {1 - {{\cos }^2}\angle ADC} = \dfrac{4\sqrt 3 }{7},\](推导中用到:$\left[a\right]$)
所以\[ \begin{split}\sin \angle BAD &= \sin \left(\angle ADC - \angle B\right) \\& \overset{\left[b\right]}= \sin \angle ADC \cdot \cos \angle B - \cos \angle ADC \cdot \sin \angle B \\& = \dfrac{4\sqrt 3 }{7} \times \dfrac{1}{2} - \dfrac{1}{7} \times \dfrac{\sqrt 3 }{2} \\& = \dfrac{3\sqrt 3 }{14} .\end{split}\](推导中用到:$\left[b\right]$) -
求 $BD,AC$ 的长.标注答案$ BD = 3 $;$ AC = 7$解析本题考查正余弦定理的简单应用.选择合适的三角形是本题的关键.在 $\triangle ABD$ 中,由正弦定理得\[\dfrac{AB}{\sin \angle ADB} = \dfrac{AD}{\sin \angle B} = \dfrac{BD}{\sin \angle BAD},\]即\[\dfrac{8}{{\dfrac{4\sqrt 3 }{7}}} = \dfrac{AD}{{\dfrac{\sqrt 3 }{2}}} = \dfrac{BD}{{\dfrac{3\sqrt 3 }{14}}},\]解得\[BD = 3,AD = 7.\]在 $\triangle ACD$ 中,由余弦定理得\[\begin{split} A{C^2} &= A{D^2} + D{C^2} - 2AD \cdot DC \cdot \cos \angle ADC \\& = {7^2} + {2^2} - 2 \times 7 \times 2 \times \dfrac{1}{7} \\& = 49 ,\end{split} \]所以 $ AC = 7$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2