小波以游戏方式决定是参加学校合唱团还是参加学校排球队,游戏规则为:以 $O$ 为起点,再从 ${A_1},{A_2},{A_3},{A_4},{A_5},{A_6},{A_7},{A_8}$(如图)这 $ 8 $ 个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为 $X$.若 $X = 0$ 就参加学校合唱团,否则就参加学校排球队.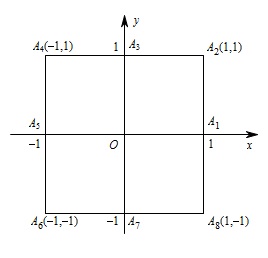

【难度】
【出处】
2013年高考江西卷(理)
【标注】
-
求小波参加学校合唱团的概率;标注答案略解析由古典概型的概率计算公式计算即可.从 $ 8 $ 个点中任取两点为向量终点的不同取法共有 $ {\mathrm{C}}_{8}^{2}=28 $ 种,当 $ X=0 $ 时,两向量夹角为直角,共有 $ 8 $ 种情形,所以小波参加学校合唱团的概率为\[ P\left( X=0 \right)=\dfrac{8}{28}=\dfrac{2}{7}. \]
-
求 $X$ 的分布列和数学期望.标注答案略解析关键是求出两向量数量积的所有可能情形及相应的概率.两向量数量积 $ X $ 的所有可能取值为 $ -2,-1,0,1 $,
$ X=-2 $ 时,有 $ 2 $ 种情形;
$ X=1 $ 时,有 $ 8 $ 种情形;
$ X=-1 $ 时,有 $ 10 $ 种情形.
所以 $ X $ 的分布列为\[\begin{array}{|c|c|c|c|c|} \hline
X & -2 & -1 & 0 & 1 \\ \hline
P & \frac{1}{14} & \frac{5}{14} & \frac{2}{7} & \frac{2}{7} \\ \hline \end{array} \\ EX=\left( -2 \right)\times \dfrac{1}{14}+\left( -1 \right)\times \dfrac{5}{14}+0\times \dfrac{2}{7}+1\times \dfrac{2}{7}=-\dfrac{3}{14}.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2