如图，四棱锥 $P - ABCD$ 中，$PA \perp $ 平面 $ABCD$，$E$ 为 $BD$ 的中点，$G$ 为 $PD$ 的中点，$\triangle DAB \cong \triangle DCB$，$EA = EB = AB = 1,PA = \dfrac{3}{2}$，连接 $CE$ 并延长交 $AD$ 于 $F$．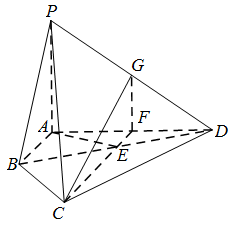
【难度】
【出处】
2013年高考江西卷（理）
【标注】
-
求证：$AD \perp $ 平面 $CFG$；标注答案略解析根据线面垂直的判定定理证明即可．在 $ \triangle ABD $ 中，因为点 $ E $ 是 $ BD $ 中点，所以\[ EA=EB=ED=AB=1 ,\]故\[ \angle BAD=\frac{\mathrm \pi} {2}, \angle ABE=\angle AEB=\frac{\mathrm \pi} {3} .\]因为 $ \triangle DAB \cong \triangle DCB $，所以 $ \triangle EAB \cong \triangle ECB $，从而有\[ \angle FED=\angle BEC=\angle AEB=\frac{\mathrm \pi} {3} ,\]所以 $ \angle FED=\angle FEA $，故 $ EF\perp AD ,AF=FD $．
又 $ PG=GD $，所以 $ FG\parallel PA $．
又 $ PA\perp $ 平面 $ ABCD $，所以 $ GF\perp AD $，故 $ AD\perp $ 平面 $ CFG $． -
求平面 $BCP$ 与平面 $DCP$ 的夹角的余弦值．标注答案略解析可以 $A$ 为原点建立空间直角坐标系，用向量法求解两平面夹角的余弦值．以点 $ A $ 为坐标原点建立如图所示的坐标系，
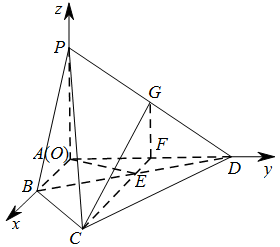则\[ A\left( 0,0,0 \right),B\left( 1,0,0 \right),C\left( \dfrac{3}{2},\dfrac{\sqrt{3}}{2},0 \right),D\left( 0,\sqrt{3},0 \right),P\left( 0,0,\dfrac{3}{2} \right). \]故\[\begin{split}\overrightarrow{BC}&=\left( \frac{1}{2},\frac{\sqrt{3}}{2},0 \right), \\
\overrightarrow{CP}&=\left( -\frac{3}{2},-\frac{\sqrt{3}}{2},\frac{3}{2} \right),\\
\overrightarrow{CD}&=\left( -\frac{3}{2},\frac{\sqrt{3}}{2},0 \right).\end{split}\]设平面 $ BCP $ 的法向量 $ \overrightarrow{{{n}_{1}}}=\left( 1,{{y}_{1}},{{z}_{1}} \right) $，则\[ \begin{split}\frac{1}{2}+\frac{\sqrt{3}}{2}{{y}_{1}}&=0, \\
-\frac{3}{2}-\frac{\sqrt{3}}{2}{{y}_{1}}+\frac{3}{2}{{z}_{1}}&=0, \end{split} \]解得\[
{{y}_{1}}=-\frac{\sqrt{3}}{3},
{{z}_{1}}=\frac{2}{3}, \]即\[ \overrightarrow{{{n}_{1}}}=\left( 1,-\frac{\sqrt{3}}{3},\frac{2}{3} \right). \]设平面 $ DCP $ 的法向量 $ \overrightarrow{{{n}_{2}}}=\left( 1,{{y}_{2}},{{z}_{2}} \right) $，则\begin{align}
& -\frac{3}{2}+\frac{\sqrt{3}}{2}{{y}_{2}}=0,\\
& -\frac{3}{2}-\frac{\sqrt{3}}{2}{{y}_{2}}+\frac{3}{2}{{z}_{2}}=0,\\
\end{align}解得\[ {{y}_{2}}=\sqrt{3}, {{z}_{2}}=2, \]即\[ \overrightarrow{{{n}_{2}}}=\left( 1,\sqrt{3},2 \right). \]从而平面 $ BCP $ 与平面 $ DCP $ 的夹角的余弦值为\[ \cos \theta =\dfrac{ \left|\overrightarrow{{{n}_{1}}}\cdot \overrightarrow{{{n}_{2}}} \right|}{ \left|\overrightarrow{{{n}_{1}}} \right| \left|\overrightarrow{{{n}_{2}}} \right|}=\dfrac{\dfrac{4}{3}}{\sqrt{\dfrac{16}{9}}\times \sqrt{8}}=\dfrac{\sqrt{2}}{4}. \]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
