如图，圆锥顶点为 $P$，底面圆心为 $O$，其母线与底面所成的角为 $22.5^\circ $．$AB$ 和 $CD$ 是底面圆 $O$ 上的两条平行的弦，轴 $OP$ 与平面 $PCD$ 所成的角为 $60^\circ $．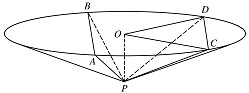
【难度】
【出处】
2013年高考安徽卷（理）
【标注】
-
证明：平面 $PAB$ 与平面 $PCD$ 的交线平行于底面；标注答案略解析根据线面平行的判定定理进行证明即可．设面 $ PAB $ 与面 $ PCD $ 的交线为 $ l $．因为 $ AB\parallel CD $，$ AB \not \subset 面 PCD $，$ CD \subset 面 PCD $，所以 $ AB\parallel 面 PCD $．又因为 $ AB\subset 面 PAB $，面 $ PAB $ 与面 $ PCD $ 的交线为 $ l $，所以 $ AB\parallel l $．由直线 $ AB $ 在底面上，而 $ l $ 在底面外可知，$ l $ 与底面平行．
-
求 $\cos \angle COD$．标注答案$ \cos \angle COD=17-12\sqrt{2}$解析先找到线面角，得出相应边的关系，再利用二倍角公式求解即可．设 $ CD $ 的中点为 $ F $，连接 $ OF$，$PF $．
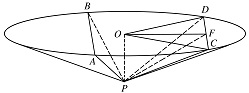由圆的性质，知\[ \angle COD=2\angle COF,OF\perp CD \]因为 $ OP\perp $ 底面，$ CD\subset $ 底面，所以 $ OP\perp CD $．
又 $ OP\cap OF=O $，故 $ CD\perp 面 OPF $．
又 $ CD\subset 面 PCD $，因此 $ 面 OPF\perp 面 PCD $，
而直线 $ OP $ 在面 $ PCD $ 上的射影为直线 $ PF $，故 $ \angle OPF $ 为 $ OP $ 与面 $ PCD $ 所成的角．由题设\[ \angle OPF=60^\circ .\]设 $ OP=h $，则\[ \begin{split}OF&=OP\cdot \tan \angle OPF \\&=\sqrt{3}h.\end{split}\]根据题设有 $ \angle OCP=22.5^\circ $，得\[ OC=\dfrac{OP}{\tan \angle OCP}=\dfrac{h}{\tan 22.5^\circ }. \]由 $ 1=\tan 45^\circ =\dfrac{2\tan 22.5^\circ }{1-{{\tan }^{2}}22.5^\circ } $和 $ \tan 22.5^\circ >0 $，可解得\[ \tan 22.5^\circ =\sqrt{2}-1, \]因此\[ OC=\dfrac{h}{\sqrt{2}-1}=\left( \sqrt{2}+1 \right)h. \]在 $ {\mathrm{Rt}}\triangle OCF $ 中，\[\begin{split} \cos \angle COF&=\dfrac{OF}{OC}\\&=\dfrac{\sqrt{3}h}{\left( \sqrt{2}+1 \right)h}\\&=\sqrt{6}-\sqrt{3}, \end{split}\]故\[\begin{split} \cos \angle COD&=\cos \left( 2\angle COF \right)\\&\overset {\left[a\right]}=2{{\cos }^{2}}\angle COF-1 \\&=17-12\sqrt{2}. \end{split}\]（推导中用到 $\left[a\right]$．）
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
