某算法的程序框图如图所示,其中输入的变量 $x$ 在 $1$,$2$,$3$,$ \cdots$,$24$ 这 $24$ 个整数中等可能随机产生.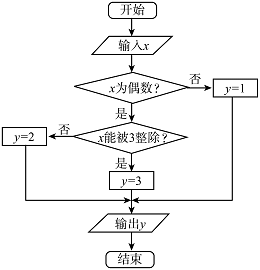

【难度】
【出处】
2013年高考四川卷(理)
【标注】
-
分别求出按程序框图正确编程运行时输出 $y$ 的值为 $i$ 的概率 ${P_i}\left( {i = 1,2,3} \right)$;标注答案输出 $y$ 的值为 $1$ 的概率为 $P_1=\dfrac{1}{2}$,输出 $y$ 的值为 $ 2 $ 的概率为 $P_2=\dfrac{1}{3}$,输出 $y$ 的值为 $ 3 $ 的概率为 $P_3=\dfrac{1}{6}$解析根据程序框图知,输入的变量是奇数时,输出的结果是 $1$,输入的变量是偶数且为 $3$ 的倍数时,输出的结果是 $3$,其他情况输出的结果是 $2$.变量 $x$ 是在 $1$,$2$,$3$,$ \cdots$,$24$ 这 $ 24 $ 个整数中随机产生的一个数,共有 $ 24 $ 种可能.根据程序框图可知,当 $x$ 从 $1$,$3$,$5$,$7$,$9$,$11$,$13$,$15$,$17$,$19$,$21$,$23$ 这 $ 12 $ 个数中产生时,输出 $y$ 的值为 $ 1 $,故\[{P_1}\overset {\left[a\right]} = \dfrac{1}{2};\](推导中用到 $ \left[a\right] $.)当 $x$ 从 $2$,$4$,$8$,$10$,$14$,$16$,$20$,$22$ 这 $ 8 $ 个数中产生时,输出 $y$ 的值为 $ 2 $,故\[{P_2} = \dfrac{1}{3};\]当 $x$ 从 $6$,$12$,$18$,$24$ 这 $ 4 $ 个数中产生时,输出 $y$ 的值为 $ 3 $,故\[{P_3} = \dfrac{1}{6}.\]所以输出 $y$ 的值为 $1$ 的概率为 $\dfrac{1}{2}$,输出 $y$ 的值为 $ 2 $ 的概率为 $\dfrac{1}{3}$,输出 $y$ 的值为 $ 3 $ 的概率为 $\dfrac{1}{6}$.
-
甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行 $n$ 次后,统计记录了输出 $y$ 的值为 $i\left( {i = 1,2,3} \right)$ 的频数.以下是甲、乙所作频数统计表的部分数据.
甲的频数统计表(部分)\[\begin{array}{|c|c|c|c|} \hline
运行次数 n & 输出 y 的值为 1 的频数 & 输出 y 的值为 2 的频数 & 输出 y 的值为 3 的频数 \\ \hline
30 & 14 & 6 & 10 \\ \hline
\cdots & \cdots & \cdots & \cdots \\ \hline
2100 & 1027 & 376 & 697 \\ \hline
\end{array}\]乙的频数统计表(部分)\[\begin{array}{|c|c|c|c|} \hline
运行次数 n & 输出 y 的值为 1 的频数 & 输出 y 的值为 2 的频数 & 输出 y 的值为 3 的频数 \\ \hline
30 & 12 & 11 & 7 \\ \hline
\cdots & \cdots & \cdots & \cdots \\ \hline
2100 & 1051 & 696 & 353 \\ \hline
\end{array}\]当 $n = 2100$ 时,根据表中的数据,分别写出甲、乙所编程序各自输出 $y$ 的值为 $i\left( {i = 1,2,3} \right)$ 的频率(用分数表示),并判断两位同学中哪一位所编写程序符合算法要求的可能性较大;标注答案当 $n = 2100$ 时,甲、乙所编程序各自输出 $y$ 的值为 $i\left( {i = 1,2,3} \right)$ 的频率如下:\[\begin{array}{|c|c|c|c|} \hline & 输出 y 的值为 1 的频率 & 输出 y 的值为 2 的频率 & 输出 y 的值为 3 的频率 \\ \hline甲 & \frac{1027}{2100} & \frac{376}{2100} & \frac{697}{2100} \\ \hline乙& \frac{1051}{2100} & \frac{696}{2100} & \frac{353}{2100} \\ \hline\end{array}\]比较频率趋势与概率,可得乙同学所编程序符合算法要求的可能性较大解析当输入次数比较大时,符合要求的算法统计的频率值应更接近其概率值,由统计数据猜测甲同学的算法可能把输出结果 $2$ 和 $3$ 的情况弄颠倒了.当 $n = 2100$ 时,甲、乙所编程序各自输出 $y$ 的值为 $i\left( {i = 1,2,3} \right)$ 的频率如下:\[\begin{array}{|c|c|c|c|} \hline & 输出 y 的值为 1 的频率 & 输出 y 的值为 2 的频率 & 输出 y 的值为 3 的频率 \\ \hline甲 & \frac{1027}{2100} & \frac{376}{2100} & \frac{697}{2100} \\ \hline乙& \frac{1051}{2100} & \frac{696}{2100} & \frac{353}{2100} \\ \hline\end{array}\]比较频率趋势与概率,可得乙同学所编程序符合算法要求的可能性较大. -
按程序框图正确编写的程序运行 $ 3 $ 次,求输出 $y$ 的值为 $2$ 的次数 $\xi $ 的分布列及数学期望.标注答案$\xi $ 的分布列为\[\begin{array}{|c|c|c|c|c|} \hline \xi & 0 & 1 & 2 & 3 \\ \hline P & \dfrac{8}{27} & \dfrac{4}{9} & \dfrac{2}{9} & \dfrac{1}{27} \\ \hline\end{array}\]$\xi $ 的数学期望为 $ 1 $解析易知 $\xi $ 服从二项分布.随机变量 $\xi $ 可能的取值为 $0$,$1$,$2$,$3$,且\[\begin{split}P\left( {\xi = 0} \right) &\overset {\left[b\right]}= {\mathrm{C}}_3^0 {\left( {\dfrac{1}{3}} \right)^0} {\left( {\dfrac{2}{3}} \right)^3} = \dfrac{8}{27}, \\ P\left( {\xi = 1} \right) &= {\mathrm{C}}_3^1 {\left( {\dfrac{1}{3}} \right)^1} {\left( {\dfrac{2}{3}} \right)^2} = \dfrac{4}{9}, \\ P\left( {\xi = 2} \right) &= {\mathrm{C}}_3^2 {\left( {\dfrac{1}{3}} \right)^2} {\left( {\dfrac{2}{3}} \right)^1} = \dfrac{2}{9}, \\ P\left( {\xi = 3} \right) &= {\mathrm{C}}_3^3 {\left( {\dfrac{1}{3}} \right)^3} {\left( {\dfrac{2}{3}} \right)^0} = \dfrac{1}{27}.\end{split}\](推导中用到 $ \left[b\right] $.)故 $\xi $ 的分布列为\[\begin{array}{|c|c|c|c|c|} \hline \xi & 0 & 1 & 2 & 3 \\ \hline P & \dfrac{8}{27} & \dfrac{4}{9} & \dfrac{2}{9} & \dfrac{1}{27} \\ \hline\end{array}\]所以\[E\xi \overset {\left[c\right]}= 0 \cdot \dfrac{8}{27} + 1 \cdot \dfrac{4}{9} + 2 \cdot \dfrac{2}{9} + 3 \cdot \dfrac{1}{27} = 1.\](推导中用到 $ \left[c\right] $.)即 $\xi $ 的数学期望为 $ 1 $.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3