如图，在三棱柱 $ABC - {A_1}{B_1}{C_{1}}$ 中，侧棱 $A{A_1} \perp 底面 ABC$，$AB = AC = 2A{A_1}$，$\angle BAC = {120^ \circ }$，$D$，${D_1}$ 分别是线段 $BC$，${B_1}{C_1}$ 的中点，$P$ 是线段 $AD$ 的中点．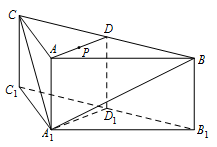
【难度】
【出处】
2013年高考四川卷（理）
【标注】
-
在平面 $ABC$ 内，试作出过点 $P$ 与平面 ${A_1}BC$ 平行的直线 $l$，说明理由，并证明直线 $l \perp 平面 AD{D_1}{A_1}$；标注答案在平面 $ABC$ 内，过点 $P$ 作直线 $l\parallel BC$，如图所示：
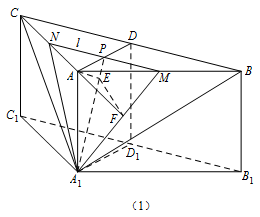理由和证明略解析根据线面平行的判定定理可作出直线 $l$，再由线面垂直的判定定理来证明．在平面 $ABC$ 内，过点 $P$ 作直线 $l\parallel BC$，如图所示： 因为 $l$ 在平面 ${A_1}BC$ 外，$BC$ 在平面 ${A_1}BC$ 内，
由直线与平面平行的判定定理可知，$l\parallel 平面 {A_1}BC$．
由已知，$AB = AC$，点 $D$ 是 $BC$ 的中点，
所以 $BC \perp AD$，则直线 $l \perp AD$．
因为 $A{A_1} \perp 平面 ABC$，所以 $A{A_1} \perp l $．
又因为 $AD$，$A{A_1}$ 在平面 $AD{D_1}{A_1}$ 内，且 $AD$ 与 $A{A_1}$ 相交，
所以直线 $l \perp 平面 AD{D_1}{A_1}$． -
设（1）中的直线 $l$ 交 $AB$ 于点 $M$，交 $AC$ 于点 $N$，求二面角 $A - {A_1}M - N$ 的余弦值．标注答案二面角 $A - {A_1}M - N$ 的余弦值为 $\dfrac{{\sqrt {15} }}{5}$解析求二面角一般有几何法和向量法，几何法的关键是作出二面角的平面角，思维难度大但运算量小；向量法的思维难度小但运算量大．方法一：
连接 ${A_1}P $，过点 $ A $ 作 $AE \perp {A_1}P $ 于点 $ E $，过点 $ E $ 作 $EF \perp {A_1}M $ 于点 $ F $，连接 $AF $．
由（1）知，$MN \perp 平面 AE{A_1} $，所以平面 $AE{A_1} \perp 平面 {A_1}MN$．
所以 $AE \perp 平面 {A_1}MN$，则 ${A_1}M \perp AE$．
所以 ${A_1}M \perp 平面 AEF$，则 ${A_1}M \perp AF$．
故 $\angle AFE$ 为二面角 $A - {A_1}M - N$ 的平面角（设为 $\theta $）．
设 $A{A_1} = 1$，则由 $AB = AC = 2A{A_1}$，$\angle BAC = 120^\circ $，有\[\angle BAD = 60^\circ ,AB = 2,AD = 1.\]又 $P$ 为 $AD$ 的中点，所以 $M$ 为 $AB$ 的中点，且\[AP = \dfrac{1}{2},AM = 1.\]所以在 $\mathrm{Rt} \triangle A{A_1}P$ 中，${A_1}P = \dfrac{\sqrt 5 }{2}$．
在 $\mathrm{Rt} \triangle {A_1}AM$ 中，${A_1}M = \sqrt 2 $．从而\begin{split}AE &= \dfrac{{A{A_1} \cdot AP}}{{{A_1}P}} = \dfrac{1}{\sqrt 5 },\\ AF &= \dfrac{{A{A_1} \cdot AM}}{{{A_1}M}} = \dfrac{1}{\sqrt 2 },\end{split}所以\[\sin \theta = \dfrac{AE}{AF} = \dfrac{\sqrt 2 }{\sqrt 5 }.\]所以\[\begin{split}\cos \theta &\overset{\left[a\right]}= \sqrt {1 - {{\sin }^2}\theta } \\&= \dfrac{{\sqrt {15} }}{5}.\end{split}\]（推导中用到 $\left[a\right]$．）故二面角 $A - {A_1}M - N$ 的余弦值为 $\dfrac{{\sqrt {15} }}{5}$．
方法二：
可以用向量法求解．设 $A{A_1}=1 $，则 $AB=AC=2 $．如图，过点 ${A_1}$ 作 ${A_1}E$ 平行于 ${C_1}{B_1}$，以点 ${A_1}$ 为坐标原点，分别以 $\overrightarrow {{A_1}E} $，$\overrightarrow {{A_1}{D_1}} $，$\overrightarrow {{A_1}A} $ 的方向为 $x$ 轴，$y$ 轴，$z$ 轴的正方向建立空间直角坐标系 $Oxyz$（点 $O$ 与点 ${A_1}$ 重合），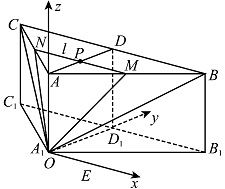
则\[{A_1}\left( {0,0,0} \right),A\left( {0,0,1} \right).\]因为 $P$ 为 $AD$ 的中点，所以 $M$，$N$ 分别为 $AB$，$AC$ 的中点，故\[M\left( {\dfrac{\sqrt 3 }{2},\dfrac{1}{2},1} \right) , N\left( { - \dfrac{\sqrt 3 }{2},\dfrac{1}{2},1} \right),\]所以\[\begin{split}\overrightarrow {{A_1}M} &= \left( {\dfrac{\sqrt 3 }{2},\dfrac{1}{2},1}\right) ,\\ \overrightarrow {A{A_1}} &= \left( {0,0,1} \right), \\ \overrightarrow {NM} &= \left( {\sqrt 3 ,0,0} \right).\end{split}\]设平面 $A{A_1}M$ 的一个法向量为 $\overrightarrow {n_1} = \left( {{x_1},{y_1},{z_1}} \right)$，则\[{\begin{cases} \overrightarrow {n_1} \perp \overrightarrow {{A_1}M} , \\ \overrightarrow {n_1} \perp \overrightarrow{{A_1}A} , \\ \end{cases}}\]即\[{\begin{cases} \overrightarrow {n_1} \cdot\overrightarrow {{A_1}M} = 0, \\ \overrightarrow {n_1} \cdot \overrightarrow{{A_1}A} = 0, \\ \end{cases}}\]故有\[{\begin{cases} \left( {{x_1},{y_1},{z_1}}\right) \cdot \left( {\dfrac{\sqrt 3 }{2},\dfrac{1}{2},1} \right) = 0, \\\left( {{x_1},{y_1},{z_1}} \right) \cdot \left( {0,0,1} \right) = 0, \\\end{cases}}\]从而\[{\begin{cases} \dfrac{\sqrt 3 }{2}{x_1} + \dfrac{1}{2}{y_1}+ {z_1} = 0, \\ {z_1} = 0. \\ \end{cases}}\]取 ${x_1} = 1$，则 ${y_1} = - \sqrt 3 $，所以\[\overrightarrow {n_1} = \left( {1, - \sqrt 3 ,0} \right).\]设平面 ${A_1}MN$ 的一个法向量为 $\overrightarrow {n_2} = \left( {{x_2},{y_2},{z_2}} \right)$，则\[{\begin{cases} \overrightarrow {n_2} \perp \overrightarrow {{A_1}M} , \\ \overrightarrow {n_2} \perp \overrightarrow {NM}, \\ \end{cases}}\]即\[{\begin{cases} \overrightarrow {n_2} \cdot \overrightarrow {{A_1}M} = 0, \\ \overrightarrow {n_2} \cdot \overrightarrow {NM} = 0, \\ \end{cases}}\]故有\[{\begin{cases} \left( {{x_2},{y_2},{z_2}}\right) \cdot \left( {\dfrac{\sqrt 3 }{2},\dfrac{1}{2},1} \right) = 0, \\\left( {{x_2},{y_2},{z_2}} \right) \cdot \left( {\sqrt 3 ,0,0} \right) = 0, \\\end{cases}}\]从而\[{\begin{cases} \dfrac{\sqrt 3 }{2}{x_2} + \dfrac{1}{2}{y_2}+ {z_2} = 0, \\ \sqrt 3 {x_2} = 0. \\ \end{cases}}\]取 ${y_2} = 2$，则 ${z_2} = - 1$，所以\[\overrightarrow {n_2} = \left( {0,2, - 1} \right).\]设二面角$A - {A_1}M - N$ 的平面角为 $\theta $，又 $\theta $ 为锐角，则\[\begin{split}\cos \theta &= \left| {\dfrac{{\overrightarrow {n_1} \cdot \overrightarrow{n_2} }}{{ \left|\overrightarrow {n_1} \right| \left|\overrightarrow {n_2} \right|}}} \right| \\&=\left| {\dfrac{{\left( {1, - \sqrt 3 ,0} \right) \cdot \left( {0,2, - 1}\right)}}{2 \cdot \sqrt 5 }} \right| \\&= \dfrac{{\sqrt {15} }}{5},\end{split}\]故二面角 $A - {A_1}M - N$ 的余弦值为 $\dfrac{{\sqrt {15} }}{5}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
